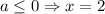1-й случай. x=2 - обращает дробь в ноль. Поэтому x=2 является решением при любом a, за исключением случая, когда поскольку в этом случае знаменатель обращается в ноль.
2-й случай. этот множитель можно отбросить. Получаем
Если числитель отрицателен, знаменатель положителен, поэтому дробь отрицательна, и решений нет.
Если числитель отрицателен, поэтому для положительности дроби нужно, чтобы знаменатель был отрицателен, .
Если a=4, дробь равна нулю; x - любой (естественно, за исключением x=2 - об этом мы говорили раньше).
Если a>4, числитель положителен, поэтому для положительности дроби нужно, чтобы знаменатель был положителен,
1-й случай. x=2 - обращает дробь в ноль. Поэтому x=2 является решением при любом a, за исключением случая, когда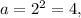
поскольку в этом случае знаменатель обращается в ноль.
2-й случай.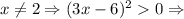
этот множитель можно отбросить. Получаем
Если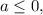
числитель отрицателен, знаменатель положителен, поэтому дробь отрицательна, и решений нет.
Если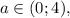
числитель отрицателен, поэтому для положительности дроби нужно, чтобы знаменатель был отрицателен, 
.
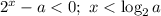Если a=4, дробь равна нулю; x - любой (естественно, за исключением x=2 - об этом мы говорили раньше).
Если a>4, числитель положителен, поэтому для положительности дроби нужно, чтобы знаменатель был положителен,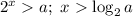
ответ: