И так, сначала умножаем все выражение на 12 (т. к. 12 это НОК по отношению к 4, 6 и 3), получается, что:
Сокращаем дроби и получаем:
Отлично, мы значительно упростили изначальное выражение и теперь нам необходимо раскрыть скобки (умножить каждый член в скобках на множитель за ними), что мы и сделаем:
Как мы видим, получается очень красиво, т. к. все дроби просто-напросто сократятся:
Снова раскроем скобки соблюдая все знаки (к знакам всегда стоит быть крайне внимательным при раскрытии скобок, так например в нашем случае раскроется как т. к. минус на минус дает плюс, а минус на плюс дает минус):
Супер, теперь уравнение приобрело совсем простой вид, проведем лишь косметические преобразования и сведем все подобные:
Переносим все неизвестные влево, а все, что известно вправо (не забываем при этом менять знаки):
Считаем:
Видим, что наше уравнение является тождеством — а это значит, что его решением является любое значение x.
И так, сначала умножаем все выражение на 12 (т. к. 12 это НОК по отношению к 4, 6 и 3), получается, что:
Сокращаем дроби и получаем:
Отлично, мы значительно упростили изначальное выражение и теперь нам необходимо раскрыть скобки (умножить каждый член в скобках на множитель за ними), что мы и сделаем:
Как мы видим, получается очень красиво, т. к. все дроби просто-напросто сократятся:
Снова раскроем скобки соблюдая все знаки (к знакам всегда стоит быть крайне внимательным при раскрытии скобок, так например в нашем случае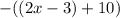 раскроется как
раскроется как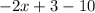 т. к. минус на минус дает плюс, а минус на плюс дает минус):
т. к. минус на минус дает плюс, а минус на плюс дает минус):
Супер, теперь уравнение приобрело совсем простой вид, проведем лишь косметические преобразования и сведем все подобные:
Переносим все неизвестные влево, а все, что известно вправо (не забываем при этом менять знаки):
Считаем:
Видим, что наше уравнение является тождеством — а это значит, что его решением является любое значение x.