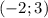Чтобы не мучаться с совокупностью двух систем, применим метод рационализации. Советую о нем почитать, так как он сильно упрощает жизнь. Конкретно здесь выражение вида по знаку эквивалентно выражению
.
Знак не поменял, так как дважды менял знак в скобках
Теперь используем метод интервалов. Я специально перед каждым x оставил коэффициент 1, здесь при каждой скобке степень равна 1, это значит, что знак при переходе через нуль функции будет меняться, а в самом крайнем правом промежутке будет "+" - нули функции.
В итоге получим x∈[-2;-1]∪[1;2]
Но мы не учли область определения неравенства
Это система из нескольких неравенств:
2-x>0 => x<2
2-x≠1 => x≠1
x+2>0 => x>-2
x+3>0 => x>-3
x+3≠1 => x≠-2
3-x>0 => x<3
Из всего этого добра как раз и получаем, что x∈(-2;-1]∪(1;+∞)
Теперь решаем следующее неравенство:
=> функция логарифма с основанием большим 1 монотонно возрастает, тогда имеет место переход к неравенству
Теперь осталось учесть область определения неравенства:
, отсюда, кстати, сразу следует, что в первом неравенстве обе скобки должны быть больше нуля, то есть
Учитывая область определения, как раз и получаем, что x∈
Объяснение:
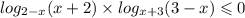
Находим область допустимых значений ( ОДЗ )Х € ( -2; 1 ) U ( 1; 2 )Рассмотрим все возможные случаи :
Фото приложено~•~•~•ZLOY_TIGROVSKIY~•~•~•1-е неравенство:
Чтобы не мучаться с совокупностью двух систем, применим метод рационализации. Советую о нем почитать, так как он сильно упрощает жизнь. Конкретно здесь выражение вида по знаку эквивалентно выражению
по знаку эквивалентно выражению 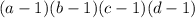
Знак не поменял, так как дважды менял знак в скобках
Теперь используем метод интервалов. Я специально перед каждым x оставил коэффициент 1, здесь при каждой скобке степень равна 1, это значит, что знак при переходе через нуль функции будет меняться, а в самом крайнем правом промежутке будет "+"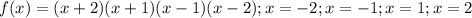 - нули функции.
- нули функции.
В итоге получим x∈[-2;-1]∪[1;2]
Но мы не учли область определения неравенства
Это система из нескольких неравенств:
2-x>0 => x<2
2-x≠1 => x≠1
x+2>0 => x>-2
x+3>0 => x>-3
x+3≠1 => x≠-2
3-x>0 => x<3
Из всего этого добра как раз и получаем, что x∈(-2;-1]∪(1;+∞)
Теперь решаем следующее неравенство:
=> функция логарифма с основанием большим 1 монотонно возрастает, тогда имеет место переход к неравенству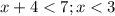
Теперь осталось учесть область определения неравенства:
Учитывая область определения, как раз и получаем, что x∈