. Решите неравенства. Соотнесите свои ответы с названиями промежутков. х2+2х+10˃ 0;
х2-12х+36 ≤ 0;
х2+3х+2 ≥ 0;
х2 - 9 ≤0;
Неравенство не имеет решений
Решением неравенства является вся числовая прямая
Решением неравенства является одна точка.
Решением неравенства является закрытый промежуток.
Решением неравенства является открытый промежуток.
Решением неравенства является объединение двух промежутков.
умоляю
25
Объяснение:
решения.
Выпишем несколько первых натуральных чисел кратных 5:
5, 10, 15, 20, 25, 30, 35, 40, 54, ... (далее каждое пятое натуральное число будет являться членом данной последовательности).
Пронумеруем члены последовательности:
Число, следующее за четвертым членом последовательности 25.
решения.
Воспользуемся формулой для нахождения n-го члена арифметической последовательности.
Наименьшее натуральное число делящееся на 5 это 5, т.е.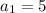 .
.
Далее каждое пятое натуральное число делится на 5. Значит разность арифметической прогрессии равна 5, т.е.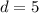 .
.
Т.к. по условию нужно найти число, следующее за a₄, то находим а₅.
-90
Объяснение:
Согласно условию задачи, дана арифметическая прогрессия аn, в которой а1 = -7.2, а2 = -6.9. Используя определение арифметической прогрессии, находим разность d данной прогрессии: d = а2 - а1 = -6.9 - (-7.2) = -6.9 + 7.2 = 0.3. Используя формулу n-го члена арифметической прогрессии аn = a1 + (n - 1) * d, найдем последний отрицательный член данной прогрессии. Для этого решим в целых числах неравенство: -7.2 + (n - 1) * 0.3 < 0; -7.2 + 0.3 * n - 0.3 < 0; -7.5 + 0.3 * n < 0; 0.3 * n < 7.5; n < 7.5 / 0.3; n < 25. Следовательно, 24-й член а24 является последним отрицательным членом данной прогрессии. Используя формулу суммы первых n членов арифметической прогрессии Sn = (2 * a1 + d * (n - 1)) * n / 2 при n = 24, найдем сумму первых 24 членов данной арифметической прогрессии: S24 = (2 * ( -7.2) + 0.3 * (24 - 1)) * 24 / 2 = (-14.4 + 6.9) * 12 = -7.5 * 12 = -90. ответ: сумма всех отрицательных членов данной арифметической прогрессии равна -90.