Найдем область допустимых значений (ОДЗ):
Следовательно,
Так как при , а , делаем вывод: данное неравенство выполняется при всех значениях из области допустимых значений.
ответ:
Найдем область допустимых значений (ОДЗ):
Следовательно,![x \in (0; \ 1]](/tpl/images/1071/9817/5fa1d.png)
Так как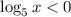 при
при ![x \in (0; \ 1]](/tpl/images/1071/9817/5fa1d.png) , а
, а 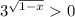 , делаем вывод: данное неравенство выполняется при всех значениях
, делаем вывод: данное неравенство выполняется при всех значениях  из области допустимых значений.
из области допустимых значений.
ответ:![x \in (0; \ 1]](/tpl/images/1071/9817/5fa1d.png)