1) x ∈ (, 1)
2) x ∈ (-∞, 2] U [4, +∞)
3) x ∈ (-∞, 2) U (3, +∞)
4) x ∈ (-4, 1)
Объяснения:
1) |3x + 1| < 4.
Рассмотрим возможные случаи:
[ 3x + 1 < 4, 3x + 1 ≥ 0 [ x < 1, x ≥
| ⇔ |
[ - (3x + 1) < 4, 3x + 1 < 0 [ x > , x <
[ x ∈ [, 1) [
| ⇔ | x ∈ (, 1)
[ x ∈ (, ) [
2) |2x - 5| ≥ x - 1
|2x - 5| - x ≥ -1
[ 2x - 5 - x ≥ - 1, 2x - 5 ≥ 0 [ x ≥ 4, x ≥
[ - (2x - 5) - x ≥ -1, 2x - 5 < 0 [ x ≤ 2, x <
[ x ∈ [4, +∞) [
| ⇔ | x ∈ (-∞, 2] U [4, +∞)
[ x ∈ (-∞, 2] [
3) |5 - 2x| > 1
[ 5 - 2x > 1, 5 - 2x ≥ 0 [ x < 2, x ≤
[ - (5 - 2x) > 1, 5 - 2x < 0 [ x > 3, x >
[ x ∈ (-∞, 2) [
| ⇔ | x ∈ (-∞, 2) U (3, +∞)
[ x ∈ (3, +∞) [
4) |x| + |x + 3| < 5
[ x + x + 3 < 5, x ≥0, x + 3 ≥ 0 [ x < 1, x ≥ 0, x ≥ -3
[ -x + x + 3 < 5, x < 0, x + 3 ≥ 0 [ x ∈ R, x < 0, x ≥ -3
[ x - (x + 3) < 5, x ≥ 0, x + 3 < 0 [ x ∈ R, x ≥ 0, x < -3
[ -x - (x+3) < 5, x <0, x + 3 < 0 [ x > -4, x < 0, x < -3
[ x < 1, x ∈ [0, +∞) [ x ∈ [0, 1) [
[ x ∈ R, x ∈ [-3,0) [ x ∈ [-3, 0) [
| ⇔ | ⇔ | x ∈ (-4, 1)
[ x ∈ R, x ∈ ∅ [ x ∈ ∅ [
[ x > -4, x ∈ (-∞, 3) [ x ∈ (-4, -3) [
1) x ∈ (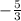 , 1)
, 1)
2) x ∈ (-∞, 2] U [4, +∞)
3) x ∈ (-∞, 2) U (3, +∞)
4) x ∈ (-4, 1)
Объяснения:
1) |3x + 1| < 4.
Рассмотрим возможные случаи:
[ 3x + 1 < 4, 3x + 1 ≥ 0 [ x < 1, x ≥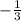
| ⇔ |
[ - (3x + 1) < 4, 3x + 1 < 0 [ x >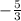 , x <
, x < 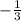
[ x ∈ [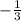 , 1) [
, 1) [
| ⇔ | x ∈ (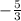 , 1)
, 1)
[ x ∈ (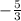 ,
, 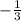 ) [
) [
2) |2x - 5| ≥ x - 1
|2x - 5| - x ≥ -1
Рассмотрим возможные случаи:
[ 2x - 5 - x ≥ - 1, 2x - 5 ≥ 0 [ x ≥ 4, x ≥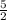
| ⇔ |
[ - (2x - 5) - x ≥ -1, 2x - 5 < 0 [ x ≤ 2, x <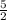
[ x ∈ [4, +∞) [
| ⇔ | x ∈ (-∞, 2] U [4, +∞)
[ x ∈ (-∞, 2] [
3) |5 - 2x| > 1
Рассмотрим возможные случаи:
[ 5 - 2x > 1, 5 - 2x ≥ 0 [ x < 2, x ≤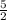
| ⇔ |
[ - (5 - 2x) > 1, 5 - 2x < 0 [ x > 3, x >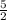
[ x ∈ (-∞, 2) [
| ⇔ | x ∈ (-∞, 2) U (3, +∞)
[ x ∈ (3, +∞) [
4) |x| + |x + 3| < 5
Рассмотрим возможные случаи:
[ x + x + 3 < 5, x ≥0, x + 3 ≥ 0 [ x < 1, x ≥ 0, x ≥ -3
[ -x + x + 3 < 5, x < 0, x + 3 ≥ 0 [ x ∈ R, x < 0, x ≥ -3
| ⇔ |
[ x - (x + 3) < 5, x ≥ 0, x + 3 < 0 [ x ∈ R, x ≥ 0, x < -3
[ -x - (x+3) < 5, x <0, x + 3 < 0 [ x > -4, x < 0, x < -3
[ x < 1, x ∈ [0, +∞) [ x ∈ [0, 1) [
[ x ∈ R, x ∈ [-3,0) [ x ∈ [-3, 0) [
| ⇔ | ⇔ | x ∈ (-4, 1)
[ x ∈ R, x ∈ ∅ [ x ∈ ∅ [
[ x > -4, x ∈ (-∞, 3) [ x ∈ (-4, -3) [