Рассмотрим функцию .
Найдем область определения функции: функция существует, когда знаменатель дроби не обращается в ноль
Найдем теперь нули функции:
ответ:
Рассмотрим функцию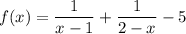 .
.
Найдем область определения функции: функция существует, когда знаменатель дроби не обращается в ноль
Найдем теперь нули функции:
ответ:![x \in \bigg(-\infty;1\bigg)\cup\left[\dfrac{15-\sqrt{5}}{10};\dfrac{15+\sqrt{5}}{10}\right]\cup\bigg(2;+\infty\bigg)](/tpl/images/0841/5548/3212e.png)