Пусть первая цифра трехзначного числа будет - а. Вторая - в Третья -с. Тогда должно выполнятся равенство 5*а*в*с=100*а+10*в+с Проанолизировав равенство получаем, что: 1)а≠0,в≠0 и с≠0 так как иначе 5*а*в*с=0 а это совсем не трехзначное число 2) с=5 Так как любое число умноженное на 5 ( 5*а*в*с ) будет оканчиватся 0 или 5 (а нуль мы уже исключили в первом пункте) 3) а и в - должны быть нечетные, так как иначе число 5*а*в*с=25*а*в будет оканчиваться нулем (если а-четное то его можно представить в виде а=2к. Значит 25*а*в=25*2*к*в=100*в, оканчивается нулем противоречит с первому) Подставим в равенство с=5 и получим значение а через в 5*а*в*с=100*а+10*в+с 25*а*в=100*а+10*в+5 25*а*в-100а=10*в+5 а(25в-100)=10*в+5 а=(10*в+5)/(25в-100) а=(2*в+1)/(5в-20) При всех в<5 Знаменатиль будет меньше или равен нулю. Поэтому эти варианты не рассматриваем. Остаются толко нечетные варианты при в=5 : а=(2*5+1)/(5*5-20)=11/5 не подходит (так как это не целочисленное решение) при в=7 : а=(2*7+1)/(5*7-20)=15/15=1 подходит при в=9 : а=(2*9+1)/(5*9-20)=19/25 не подходит Единственное решение - 175
ответ: 8) n=4 или n=5
Объяснение:
дробь правильная, если числитель меньше знаменателя...
n²-n+15 < 7n+3
n²-8n+12 < 0 корни по т.Виета (2) и (6);
решение "между корнями": n ∈ (2; 6),
т.е. n∈N (по условию) может быть равно: {3; 4; 5}
остальное (сократима ли дробь) проще посчитать...
n=3: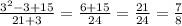
дробь сократима...
n=4: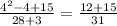
дробь НЕсократима (31-простое число))
n=5: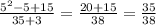
дробь НЕсократима...
решение задачи 9) на рисунке...
таких окружностей две...
касание может быть как внутренним, так и внешним...
точки касания окружностей лежат на линии центров...
Вторая - в
Третья -с.
Тогда должно выполнятся равенство
5*а*в*с=100*а+10*в+с
Проанолизировав равенство получаем, что:
1)а≠0,в≠0 и с≠0 так как иначе 5*а*в*с=0 а это совсем не трехзначное число
2) с=5 Так как любое число умноженное на 5 ( 5*а*в*с )
будет оканчиватся 0 или 5 (а нуль мы уже исключили в первом пункте)
3) а и в - должны быть нечетные, так как иначе число 5*а*в*с=25*а*в
будет оканчиваться нулем
(если а-четное то его можно представить в виде
а=2к. Значит 25*а*в=25*2*к*в=100*в, оканчивается нулем
противоречит с первому)
Подставим в равенство с=5 и получим значение а через в
5*а*в*с=100*а+10*в+с
25*а*в=100*а+10*в+5
25*а*в-100а=10*в+5
а(25в-100)=10*в+5
а=(10*в+5)/(25в-100)
а=(2*в+1)/(5в-20)
При всех в<5 Знаменатиль будет меньше или равен нулю.
Поэтому эти варианты не рассматриваем.
Остаются толко нечетные варианты
при в=5 : а=(2*5+1)/(5*5-20)=11/5 не подходит
(так как это не целочисленное решение)
при в=7 : а=(2*7+1)/(5*7-20)=15/15=1 подходит
при в=9 : а=(2*9+1)/(5*9-20)=19/25 не подходит
Единственное решение - 175