Для начала разложим знаменатель на множители, для этого найдем корни уравнения
x²+6x+5=0
x₁=(-3+4)/2=1/2; x₂=(-3-4)/2=-7/2
Тогда:
a) при x=-1 знаменатель дроби ≠0, а значит функция непрерывна в этой точке и определена
:
b) при x=-5 знаменатель дроби также ≠0
c) Асимптоты (вертикальные) будут при x=x₁, x₂, когда знаменатель=0.
Чертеж - на рисунке.
d) Наклонная асимптота определяется:
При x→∞ можно оставить в числителе и знаменателе только старшие степени:
отсюда: k=1, b=0
И наклонная асимптота имеет зависимость: y=x.
ответ: 1/6
Объяснение: для начала выведем формулу самой прямой.
Пусть прямая, проходящая через заданные точки, имеет вид у = kx + b.
По условию y(1) = 0, y(0) = -3.
1)1 · k + b =0, k + b = 0 ⇒ k = -b.
2)0·k + b = -3. b = -3 ⇒ k = 3.
Исходная прямая - y = 3x - 3.
Теперь исследуем функцию y = -x² + 4x - 3. График - парабола, ветви направлены вниз.
Нули функции - x = 1 и x = 3. Вершина: x = -b/2a = -4/-2=2, y=-2²+8-3=-4+5=1. (2; 1) Нам этого достаточно.
Строим графики (во вложении. Фигура, площадь которой нужно найти, заштрихована красным).
Площадь фигуры будем искать на отрезке [0; 1]
По формуле где f(x) ≥ g(x) (т.е. график функции f выше графика функции g) находим искомую площадь:
Искомая площадь - S = 1/6 (кв. ед)
Для начала разложим знаменатель на множители, для этого найдем корни уравнения
x²+6x+5=0
x₁=(-3+4)/2=1/2; x₂=(-3-4)/2=-7/2
Тогда:
a) при x=-1 знаменатель дроби ≠0, а значит функция непрерывна в этой точке и определена
b) при x=-5 знаменатель дроби также ≠0
c) Асимптоты (вертикальные) будут при x=x₁, x₂, когда знаменатель=0.
Чертеж - на рисунке.
d) Наклонная асимптота определяется:
При x→∞ можно оставить в числителе и знаменателе только старшие степени:
отсюда: k=1, b=0
И наклонная асимптота имеет зависимость: y=x.
ответ: 1/6
Объяснение: для начала выведем формулу самой прямой.
Пусть прямая, проходящая через заданные точки, имеет вид у = kx + b.
По условию y(1) = 0, y(0) = -3.
1)1 · k + b =0, k + b = 0 ⇒ k = -b.
2)0·k + b = -3. b = -3 ⇒ k = 3.
Исходная прямая - y = 3x - 3.
Теперь исследуем функцию y = -x² + 4x - 3. График - парабола, ветви направлены вниз.
Нули функции - x = 1 и x = 3. Вершина: x = -b/2a = -4/-2=2, y=-2²+8-3=-4+5=1. (2; 1) Нам этого достаточно.
Строим графики (во вложении. Фигура, площадь которой нужно найти, заштрихована красным).
Площадь фигуры будем искать на отрезке [0; 1]
По формуле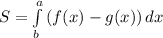 где f(x) ≥ g(x) (т.е. график функции f выше графика функции g) находим искомую площадь:
где f(x) ≥ g(x) (т.е. график функции f выше графика функции g) находим искомую площадь:
Искомая площадь - S = 1/6 (кв. ед)