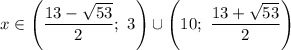Объяснение:
ОДЗ: x²-13x+30>0
D= 169-120= 49
x1= (13-7)/2= 3
x2= (13+7)/2= 10
(x-3)(x-10)>0
x∈(-∞;3)∪(10;+∞)
x²-13x+30<1
x²-13x+29<0
D= 169- 116=53
x1= (13-√53)/2
x2= (13+√53)/2
x∈((13-√53)/2;(13+√53)/2)
пересекаем с ОДЗ и получаем ответ: x∈((13-√53)/2;3)∪(10;(13+√53)/2)
Данное неравенство равносильно системе неравенств:
Находим пересечение решений неравенств и
ответ:
Объяснение:
ОДЗ: x²-13x+30>0
D= 169-120= 49
x1= (13-7)/2= 3
x2= (13+7)/2= 10
(x-3)(x-10)>0
x∈(-∞;3)∪(10;+∞)
x²-13x+30<1
x²-13x+29<0
D= 169- 116=53
x1= (13-√53)/2
x2= (13+√53)/2
x∈((13-√53)/2;(13+√53)/2)
пересекаем с ОДЗ и получаем ответ: x∈((13-√53)/2;3)∪(10;(13+√53)/2)
Данное неравенство равносильно системе неравенств:
Находим пересечение решений неравенств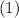 и
и 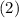
ответ: