Группа точек имеют одинаковую абсциссу х=4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид .
.
Группа точек имеют одинаковую абсциссу х=2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид .
.
Группа точек имеют одинаковую абсциссу х= -2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид .
.
Группа точек имеют одинаковую абсциссу х= -4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид .
.
Точки, имеющие одинаковую абсциссу, на координатной плоскости лежат на одной прямой, параллельной оси ОУ.
Уравнение такой прямой имеет вид это число (константа- постоянная величина ) .
Желтых 4 ж. зеленых --- 6 ж. взято 3 ж. Р(1 др.) ? Решение. 1-ы й с п о с о б. 4 + 6 = 10 всего жетонов. Р(все жел.) = (4/10)*(3/9)*(2/8) = 1/30 Р(все зел.) = (6/10)*(5/9)*(4/8) = 1/6 События вынимания жетона в очередной раз того же цвета не зависят друг от друга, поэтому их вероятности перемножаются. Но с каждым разом вероятности вынуть жетон опять того же цвета уменьшается, т.к. жетоны назад не возвращаются, Становится меньше и жетонов этого цвета, и вообще меньше жетонов. Вероятность вынимания жетонов одного цвета складывается из вероятности вынуть все зеленые или все желтые. Р(один.) = Р(все жел.) + Р(все зел.) = 1/30 + 1/6 = (5+1)/30 = 6/30 = 1/5 = 0,2 Суммарная вероятность вынуть 3 жетона с окраской равна 1 (других цветов и неокрашенных жетонов нет), она складывается из вероятностей вынуть какой-то набор. Вероятность трех одинаковых найдена. Для вычисления вероятности того, в наборе будут представлены оба цвета, надо из 1 вычесть вероятность трех одинаковых. Р(1 др.) = 1 - Р(один.) = 1 - 0,2 = 0,8 ответ:0,8 2-о й с п о с о б. 4 + 6 = 10 всего жетонов. С₁₀³ = 10!/(3!(10-3)!) = 10!/(3!*7!) = (10*9*8*7!)/(1*2*3*7!)=120 всего вынуть три жетона из десяти С₄² * С₆¹ = (4!/(2!*2!))*(6!/(1*5!)) = ((4*3*2)/(2*2))*((6*5!)/5!)) = 36 всего вынуть два желтых и один зеленый жетон. С₆² * С₄¹ = (6!/(2!*4!))*(4!/3!) = ((6*5*4!)/(2*4!))*(4*3!/3!) = 60 всего вынуть два зеленых жетона и один желтый 36 + 60 = 96 всего благоприятных дающих нужный результат). Р(1 др.) = 96/120 = 8/10 = 0,8 вероятность появления жетона другого цвета в наборе из трех вынутых . ответ:0,8
Группа точек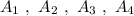
имеют одинаковую абсциссу х=4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
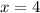Группа точек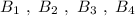
имеют одинаковую абсциссу х=2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
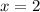Группа точек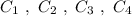
имеют одинаковую абсциссу х= -2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
Группа точек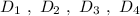
имеют одинаковую абсциссу х= -4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 
.
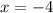Точки, имеющие одинаковую абсциссу, на координатной плоскости лежат на одной прямой, параллельной оси ОУ.
Уравнение такой прямой имеет вид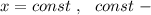
это число (константа- постоянная величина ) .
зеленых --- 6 ж.
взято 3 ж.
Р(1 др.) ?
Решение.
1-ы й с п о с о б.
4 + 6 = 10 всего жетонов.
Р(все жел.) = (4/10)*(3/9)*(2/8) = 1/30
Р(все зел.) = (6/10)*(5/9)*(4/8) = 1/6
События вынимания жетона в очередной раз того же цвета не зависят друг от друга, поэтому их вероятности перемножаются. Но с каждым разом вероятности вынуть жетон опять того же цвета уменьшается, т.к. жетоны назад не возвращаются, Становится меньше и жетонов этого цвета, и вообще меньше жетонов.
Вероятность вынимания жетонов одного цвета складывается из вероятности вынуть все зеленые или все желтые.
Р(один.) = Р(все жел.) + Р(все зел.) = 1/30 + 1/6 = (5+1)/30 = 6/30 = 1/5 = 0,2
Суммарная вероятность вынуть 3 жетона с окраской равна 1 (других цветов и неокрашенных жетонов нет), она складывается из вероятностей вынуть какой-то набор. Вероятность трех одинаковых найдена. Для вычисления вероятности того, в наборе будут представлены оба цвета, надо из 1 вычесть вероятность трех одинаковых.
Р(1 др.) = 1 - Р(один.) = 1 - 0,2 = 0,8
ответ:0,8
2-о й с п о с о б.
4 + 6 = 10 всего жетонов.
С₁₀³ = 10!/(3!(10-3)!) = 10!/(3!*7!) = (10*9*8*7!)/(1*2*3*7!)=120 всего вынуть три жетона из десяти
С₄² * С₆¹ = (4!/(2!*2!))*(6!/(1*5!)) = ((4*3*2)/(2*2))*((6*5!)/5!)) = 36 всего вынуть два желтых и один зеленый жетон.
С₆² * С₄¹ = (6!/(2!*4!))*(4!/3!) = ((6*5*4!)/(2*4!))*(4*3!/3!) = 60 всего вынуть два зеленых жетона и один желтый
36 + 60 = 96 всего благоприятных дающих нужный результат).
Р(1 др.) = 96/120 = 8/10 = 0,8 вероятность появления жетона другого цвета в наборе из трех вынутых .
ответ:0,8