x€(5;5+)
Объяснение:
(x-5)²<(x-5); переносим левую часть на правую с противоположным знаком
(x-5)²-(x-5)<0; выносим за скобку х-5 и получим: (x-5)*((x-5)-)<0
(x-5)*(x-5-)<0; теперь методом интервала решаем неравенство и получим: 5<x<5+
(х-5)^2<корень7(х-5)
(х-5)^2-корень7(х-5)<0
(х-5)×(х-5-корень7) <0
{х-5<0
{х-5-корень7>0
{х-5>0
{х-5-корень7<0
{х<5
{х>5+корень7
{х>5
{х<5+корень7
Х нет обьдинения
Х€( 5; 5+ корень7)
ответ : х€( 5; 5+корень7)
x€(5;5+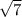 )
)
Объяснение:
(x-5)²<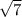 (x-5); переносим левую часть на правую с противоположным знаком
(x-5); переносим левую часть на правую с противоположным знаком
(x-5)²-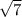 (x-5)<0; выносим за скобку х-5 и получим: (x-5)*((x-5)-
(x-5)<0; выносим за скобку х-5 и получим: (x-5)*((x-5)-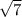 )<0
)<0
(x-5)*(x-5-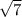 )<0; теперь методом интервала решаем неравенство и получим: 5<x<5+
)<0; теперь методом интервала решаем неравенство и получим: 5<x<5+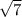
x€(5;5+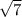 )
)
Объяснение:
(х-5)^2<корень7(х-5)
(х-5)^2-корень7(х-5)<0
(х-5)×(х-5-корень7) <0
{х-5<0
{х-5-корень7>0
{х-5>0
{х-5-корень7<0
{х<5
{х>5+корень7
{х>5
{х<5+корень7
Х нет обьдинения
Х€( 5; 5+ корень7)
ответ : х€( 5; 5+корень7)