Чтобы изобразить график линейной функции вида где и — коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
Для этого строят таблицу для двух точек: первая строка — абсцисса (иксы), вторая строка — ордината (игреки). Вы — хозяин своей таблицы. Подбирайте любое значение подставляйте его в функцию и находите (Подбирайте числа в пределах разумного.)
Пример. Изобразить график линейной функции
Строим таблицу для двух точек:
Пусть
Тогда
Пусть
Тогда
Имеем заполненную таблицу для двух точек. Изобразим координатную плоскость, отметим две точки: и — и проведем через них прямую (см. вложение). График линейной функции построен.
Если шифр пятизначный, то зафиксировав на втором месте цифру 5, а на последнем - цифру 0, получаем общее количество кодов для составления шифра замка: 5*1*5*5*1= 125 (Пояснение. Имеем 5 цифр. На первое место можно поставить любую из имеющихся пяти цифр, т.е. 7,8,5,1 и 0. Второе место "занято" цифрой 5, т.е. всего один вариант. На третье и на четвёртое место можно поставить любую из имеющихся пяти цифр (см. рассуждение выше). На последнем месте - единственный вариант - цифра ноль). Осталось только перемножить полученные варианты и вывести результат)
Чтобы изобразить график линейной функции вида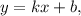
где 
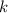и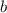 
— коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
Для этого строят таблицу для двух точек: первая строка — абсцисса (иксы), вторая строка — ордината (игреки). Вы — хозяин своей таблицы. Подбирайте любое значение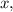
подставляйте его в функцию и находите 
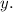(Подбирайте числа в пределах разумного.)
Пример. Изобразить график линейной функции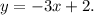
Строим таблицу для двух точек:
Пусть
Тогда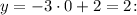
Пусть
Тогда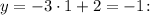
Имеем заполненную таблицу для двух точек. Изобразим координатную плоскость, отметим две точк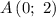и:
и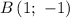 
— и проведем через них прямую (см. вложение). График линейной функции 
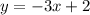построен.
(Пояснение. Имеем 5 цифр. На первое место можно поставить любую из имеющихся пяти цифр, т.е. 7,8,5,1 и 0. Второе место "занято" цифрой 5, т.е. всего один вариант. На третье и на четвёртое место можно поставить любую из имеющихся пяти цифр (см. рассуждение выше). На последнем месте - единственный вариант - цифра ноль). Осталось только перемножить полученные варианты и вывести результат)