Алгебра: Решите неравенство (x^2+2x)^2-2(x+1)^2-1 меньше равно 0

Решите неравенство (x^2+2x)^2-2(x+1)^2-1 меньше равно 0

Показать ответ

Ответ:

fdnk1

12.01.2020 05:00

На изображениях все 4 параболы.

Изображение 1

График функции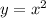 y = x^2 . Так как значение положительное (), то ветви смотрят вверх. Вершина параболы находится в точке (0; 0) .

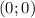Изображение 2

График функции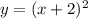 y = (x + 2)^2 . Ветви смотрят вверх, парабола смещена на 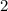влево. Вершина параболы находится в точке (-2; 0) .

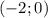Смещаем на 2 клетки влево и строим параболу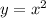 y = x^2 .

Изображение 3

График функции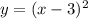 y = (x - 3)^2 . Ветви смотрят вверх, парабола смещена на 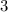вправо. Вершина параболы находится в точке (3; 0) .

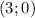Смещаем на 3 клетки вправо и строим параболу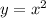 y = x^2 .

Изображение 4

График функции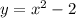 y = x^2 - 2 . Ветви смотрят вверх, парабола смещена на 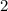вниз. Вершина параболы находится в точке (0; -2) .

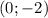Смещаем на 2 клетки вниз и строим параболу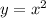 y = x^2 .

С шаблона параболы y=x² постройте график функции y=(x+2)²y=(x-3)²y=x²-2

0,0(0 оценок)

Ответ:

Mellisa11111111

11.02.2022 21:26

Объяснение:

Для начала избавляемся от дробей, то есть находим найменьшее общее кратное (в первом примере у нас это 6).

Дальше раскрываем скобки.

Переносим X в левую часть уравнения и просто числа в правую часть (важно не забывать, что при переходе через знак =, >, <, число меняет свой знак (с положительного на отрицательное и с отрицательного на положительное))

Далее находим X в системе и наносим их на прямую, дугами отмечаем в какую сторону X будет уходить в бесконечность ∞.

Пишем ответ в виде:

x є (принадлежит) ( [ скобка, если число не точное, то есть 'больше или равно' или 'меньше или равно') ( (скобка, если число точное, сторогое).

Второй пример разбирать не буду, выполняем те же действия.

По тех кто разбирается проверить моё решение на наличие ошибок