log1/22(22x-2)≥0
22x-2≥1 22x-2>0
22x≥3 x>2/22
x≥3/22 x>1/11
x∈(1/11;3/22]
log1/2(5x-8)>1
5x-8>1/2 5x-8>0
5x>8.5 x>8/5
x>1.7 x>1.6
x∈(1.6;1.7)
log24x+log24(x-23)<1 x>0
log24x(x-23)<1 x-23>0
x²-23x<24 x>23
x²-23x-24<0
D=529+96=625
x₁,₂=23±25/2=24;-1
x∈(-1;23)
Объяснение:
Выделим в левой части полный квадрат. Для этого прибавим к обеим частям уравнения выражение и перенесем слагаемое в левую часть:
1)
Тогда примет вид
Левая часть неотрицательна. Правая часть, учитывая рассматриваемый интервал, строго отрицательна. Значит, корней на данном интервале нет.
2)
Возможны 2 случая:
2.1)
Оба корня принадлежат рассматриваемому интервалу, а значит являются корнями исходного уравнения.
2.2)
То есть корень не принадлежит рассматриваемому интервалу.
log1/22(22x-2)≥0
22x-2≥1 22x-2>0
22x≥3 x>2/22
x≥3/22 x>1/11
x∈(1/11;3/22]
log1/2(5x-8)>1
5x-8>1/2 5x-8>0
5x>8.5 x>8/5
x>1.7 x>1.6
x∈(1.6;1.7)
log24x+log24(x-23)<1 x>0
log24x(x-23)<1 x-23>0
x²-23x<24 x>23
x²-23x-24<0
D=529+96=625
x₁,₂=23±25/2=24;-1
x∈(-1;23)
Объяснение:
Выделим в левой части полный квадрат. Для этого прибавим к обеим частям уравнения выражение
и перенесем слагаемое 
в левую часть:
1)
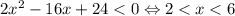
Тогда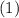
примет вид
Левая часть неотрицательна. Правая часть, учитывая рассматриваемый интервал, строго отрицательна. Значит, корней на данном интервале нет.
2)
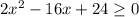
Возможны 2 случая:
2.1)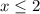
Тогда
примет вид
Оба корня принадлежат рассматриваемому интервалу, а значит являются корнями исходного уравнения.
2.2)
Тогда
примет вид
То есть корень не принадлежит рассматриваемому интервалу.