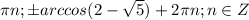Войти Регистрация Спроси ai-bota

Решите очень
2sin2x+sin^3x=0

Показать ответ

Ответ:

Sashacat555

15.10.2020 13:41

$2sin2x+sin^3x=0\\2*2sinxcosx+sin^3x=0\\sinx(4cosx+sin^2x)=0\\sinx(4cosx+1-cos^2x)=0$

$sinx=0: x=\pi n, n\in{Z}$

или

$4cosx+1-cos^2x=0\\cos^2x-4cosx-1=0\\D=16+4=20\\cosx=\frac{4\pm\sqrt{20} }{2}\\ cosx=\frac{4\pm2\sqrt{5} }{2}\\cosx=2\pm\sqrt{5}$

$cosx=2+\sqrt{5}$ - решений не имеет, так как $|cosx|\leq 1$ , а $2+\sqrt{5}1$

$cosx=2-\sqrt{5}: x=\pm{arccos(2-\sqrt{5} )}+2\pi n, n\in{Z}$

ответ: $\pi n;\pm{arccos(2-\sqrt{5} )}+2\pi n; n\in{Z}$

0,0(0 оценок)

Популярные вопросы: Алгебра

magasadrudinov

24.06.2020 11:14

Если угол при вершине на 15° меньше угла при основании,то в равнобедренном треугольнике угол при основании равен. ...

daниил1

01.11.2020 20:47

-2x+5y=-10 решите уравнение 3-мя...

habman

15.01.2020 09:15

Знайдіть сьомий член геометричної прогресії якщо b³= -8, q= -2 До ть будь ласка...

Yachit68

12.11.2021 06:52

Подайте число в стандартному вигляді: 609,4;...

sayana7

15.03.2020 08:14

решить. Упрости выражение....

solmazmitok

29.12.2020 08:59

Cos a + sin a=0,8. Найдите cos^3 a + sin^3 a...

mukhamedinaguls

01.09.2022 23:50

Разложить на множители a) (a-b)²-(a-b)(a+b) б) b²(a-1)-a²(b-1)...

DashaCat02

26.12.2022 03:43

5^(x+4)+3*4^(x+3)=4^(x+4)+4*5^(x+3)...

gratem04

26.12.2022 03:43

Решите неравенство методом параболы 2x^2-7x+6 o на листочке...

kskdosms

27.06.2022 09:29

Найдите область определения функции: y=(x-2/√(20-8x-x^2))+√(x+6)...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку