Для того, чтобы начать решать эту задачу, нам необходимо найти такую последовательность, которая приносила бы нам всегда удачу! Из условия ясно, что начинающий должен ходить первый. Можно предложить такой вариант ходов: Начинающий должен взять один карандаш. Остается 17 штук. Какое бы количество карандашей ни взял противник, обязательно нужно оставить 13 карандашей на столе. По такому же раскладу, надо оставить 9 карандашей, а затем 5. Какое бы количество карандашей не взял соперник, начинающий всегда сможет оставить ему 1 карандаш.
Для того, чтобы начать решать эту задачу, нам необходимо найти такую последовательность, которая приносила бы нам всегда удачу! Из условия ясно, что начинающий должен ходить первый. Можно предложить такой вариант ходов:
Начинающий должен взять один карандаш. Остается 17 штук. Какое бы количество карандашей ни взял противник, обязательно нужно оставить 13 карандашей на столе. По такому же раскладу, надо оставить 9 карандашей, а затем 5. Какое бы количество карандашей не взял соперник, начинающий всегда сможет оставить ему 1 карандаш.
Воспользуемся формулой разности кубов:
Выносим за скобки общий множитель:
Уравнение распадается на два. Решаем первое:
Почленно разделим на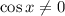 :
:
Решаем второе уравнение:
Заметим в левой части основное тригонометрическое тождество:
Обе части уравнения домножим на 2:
Чтобы в левой части применить формулу синуса двойного угла:
Но так как синус любого угла принимает значения только из отрезка от -1 до 1, то последнее уравнение не имеет решение.
Значит, никаких других корней, кроме найденных ранее, исходное уравнение не имеет.
ответ: