Нам задано линейное уравнение с двумя переменными 12х + 4у = 48. Для того, чтобы найти значение переменной х при условии, что у принимает значение равное нулю, подставим вместо у в уравнение значение равное 0 и решим полученное линейное уравнение относительно переменной х.
Подставляем у = 0,
12х + 4 * 0 = 48;
12х + 0 = 48;
12х = 48.
Разделим обе части уравнения на 12, тем самым избавимся от коэффициента перед переменной х.
a) Вероятность взять один синий карандаш, равна 5/9. В коробке останется 8 карандашей. Вероятность взять второй синий карандаш, равна 4/8 = 1/2, вероятность взять третий сини карандаш равна 3/7. По теореме умножения, 5/9 * 1/2 * 3/7 = 5/42
Аналогично вероятность взять один красный карандаш равна 4/9, второй красный карандаш - 3/8, третий красный карандаш - 2/7. По теореме умножения, 4/9 * 3/8 * 2/7 = 1/21
По теореме сложения, вероятность взять 3 карандаша одинакового цвета равна 5/42 + 1/21 = 5/42 + 2/42 = 7/42 = 1/6
б) Всего всевозможных исходов: из них нужно взять 2 синих и 1 красный карандаш, таких у нас . Вероятность того, что среди отобранных 3 карандаша 2 синих и 1 красный карандаш, равна 40/84 = 10/21
c) Вероятность того, что среди наугад выбранных 3 карандаша нет синего цвета, равна 1/21 (посчитали в пункте а), тогда вероятность того, что среди них будет хотя бы 1 карандаш синий, равна 1 - 1/21 = 20/21
х = I = 4.
Объяснение:
Нам задано линейное уравнение с двумя переменными 12х + 4у = 48. Для того, чтобы найти значение переменной х при условии, что у принимает значение равное нулю, подставим вместо у в уравнение значение равное 0 и решим полученное линейное уравнение относительно переменной х.
Подставляем у = 0,
12х + 4 * 0 = 48;
12х + 0 = 48;
12х = 48.
Разделим обе части уравнения на 12, тем самым избавимся от коэффициента перед переменной х.
Итак,
х = 48 : 12;
х = 4.
ответ: при у = 0 х принимает значение равное 4.
a) Вероятность взять один синий карандаш, равна 5/9. В коробке останется 8 карандашей. Вероятность взять второй синий карандаш, равна 4/8 = 1/2, вероятность взять третий сини карандаш равна 3/7. По теореме умножения, 5/9 * 1/2 * 3/7 = 5/42
Аналогично вероятность взять один красный карандаш равна 4/9, второй красный карандаш - 3/8, третий красный карандаш - 2/7. По теореме умножения, 4/9 * 3/8 * 2/7 = 1/21
По теореме сложения, вероятность взять 3 карандаша одинакового цвета равна 5/42 + 1/21 = 5/42 + 2/42 = 7/42 = 1/6
б) Всего всевозможных исходов: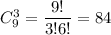
из них нужно взять 2 синих и 1 красный карандаш, таких у нас 
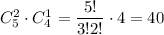. Вероятность того, что среди отобранных 3 карандаша 2 синих и 1 красный карандаш, равна 40/84 = 10/21
c) Вероятность того, что среди наугад выбранных 3 карандаша нет синего цвета, равна 1/21 (посчитали в пункте а), тогда вероятность того, что среди них будет хотя бы 1 карандаш синий, равна 1 - 1/21 = 20/21