Решите по действиям :
—9,6 : 12 – 29 :(-5,8) + 4: (-25);

Объяснение:

Участвовало всего: 76 человек.

В обеих олимпиадах: 15 человек.

Следовательно, из 76 человек

15 - дважды принимали участие

76-15 = 61 чел. - только 1 раз

Пусть,

х - число участников по математике

у - число участников по физике

Причем, очевидно что без учета 15 принимавших участие в обеих олимпиадах имеем:

(х-15)+(у-15)=61

х+у-30=61

х+у=91

Выразим х и у по отдельности:

х = 91-у

у= 91-х

Т.к. х, у - это число участников, то эти числа должны быть целыми.

И если предположить, что допустим

х - меньше 46, то

при х < 46 этот х может быть равен 45, 44 и т.д

Поэтому при целых значениях

х < 46, равнозначно неравенству х ≤ 45.

Т.е. при х ≤ 45:

х = 91 - у

91 - у ≤ 45

91 - 45 ≤ у

у ≥ 91 - 45

у ≥ 46

А при у < 46, (при у ≤ 45)

у = 91 - х

91 - х ≤ 45

х ≥ 46

Как мы видим, при любых значениях х или у одно из них обязательно будет равно или больше 46

А значит, в какой-то олимпиаде обязательно приняли участие не менее 46 человек.

Ч.Т.Д.

Объяснение:

Рассмотрим сначала первое неравенство системы.

Начнем с ОДЗ:

Продолжим решение:

1)

Замена: .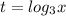

Обратная замена:

С учетом ОДЗ оба корня подходят.

2)

С учетом ОДЗ получим, что решение неравенства:

Теперь перейдем ко второму неравенству системы:

Понятно, что сначала нужно написать ОДЗ.

Продолжим решение:

Заметим, что данное неравенство хорошо раскладывается на множители:

Решим неравенство по методу интервалов.

1)

2)

Введем функци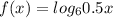и и 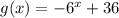. Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно, 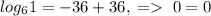, верно. Так, мы решили это уравнение, получив, что его корень x=2.

Тогда решение неравенства с учетом ОДЗ:

Итого имеем:

Найдем пересечение:

Задание выполнено!