Рассмотрим функцию:
Область определения функции: D(f)=
Если 0 < x < 1, то выражение, стоящее слева, будет всегда отрицательным, выполнено.
Если x > 1, то и применимо неравенство Коши (или неравенство о среднем):
При этом равенство достигается при откуда
Объединяя решения, получим x ∈ (0;1) ∪ {2}.
Рассмотрим функцию: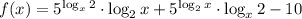
Область определения функции: D(f)=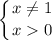
Если 0 < x < 1, то выражение, стоящее слева, будет всегда отрицательным, выполнено.
Если x > 1, то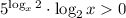
и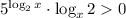 
применимо неравенство Коши (или неравенство о среднем):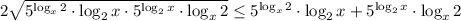 
При этом равенство достигается при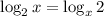
откуда
Объединяя решения, получим x ∈ (0;1) ∪ {2}.