Задача. Двое рабочих изготавливают детали. Первый работал 5 ч., второй 8 ч. — и вместе выполнили 140 деталей. При этом первый за 2 ч. изготовит на 6 деталей меньше, чем второй за 3 ч. Сколько деталей за час выполняет каждый из них?
Решение. Пусть первый рабочий за час изготовлял деталей, а второй рабочий деталей. Суммарный их объём работы (по формуле , как в задачах на движение) составит .
Второе условие запишется так:
Сложим эти два уравнения в систему:
Умножим первое уравнение на 2, а второе на –5, и сложим их:
ответ: первый рабочий за час изготавливает 12 деталей, а второй — 10 деталей.
5.
Объяснение:
|x−5| ≤ −a^6
Заметим, что выражение в левой части по определению неотрицательное.
|x−5l ≥ 0 при всех значениях х.
Выражение, записанное в правой части, неположительное, т.к. показатель степени чётный,
- а^6 ≤ 0 при любых значениях а.
Получили, что вариант |x−5| < −a^6 невозможен. Возможно лишь одновременное равенство нулю обеих частей.
|x−5| = 0
х - 5 = 0
х = 0 + 5
х = 5.
Коротко записать решение можно так:
|x−5| ≤ −a^6
Т. к. |x−5l ≥ 0, а - а^6 ≤ 0 при всех значениях переменных, то
|x−5| = 0
х - 5 = 0
х = 0 + 5
х = 5
ответ: 5.
Задача. Двое рабочих изготавливают детали. Первый работал 5 ч., второй 8 ч. — и вместе выполнили 140 деталей. При этом первый за 2 ч. изготовит на 6 деталей меньше, чем второй за 3 ч. Сколько деталей за час выполняет каждый из них?
Решение. Пусть первый рабочий за час изготовлял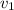
деталей, а второй рабочий 
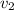деталей. Суммарный их объём работы (по формуле 
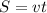, как в задачах на движение) составит 
.
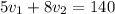Второе условие запишется так: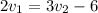
Сложим эти два уравнения в систему:
Умножим первое уравнение на 2, а второе на –5, и сложим их:
ответ: первый рабочий за час изготавливает 12 деталей, а второй — 10 деталей.