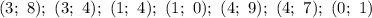Объяснение:
f(x) = x^2021 + a - заданная прямая функция.
f^(-1) (x) = корень 2021 степени из (x-a) - обратная функция.
Обратная функция имеет график, симметричный данному относительно прямой y = x.
Графики функции и обратной могут пересекаться только на прямой y = x.
Это значит, что функция сама должна пересекаться с прямой y = x.
Решаем уравнение и находим х при любом параметре а:
y = x^2021 + a = x
x = x^2021 + a
x^2021 - x + a = 0
Любой многочлен нечётной степени всегда имеет хотя бы один корень.
Поэтому при любом значении а будет хотя бы одно решение.
Преобразуем уравнение:
Если и - целые числа, то и выражения и также являются целыми.
Тогда, выражения и соответствуют квадратам целых чисел.
Если , то - но число 5 не является квадратом
целого числа, поэтому этот вариант не реализуется.
Если , то .
Если , то - эти варианты также не реализуются, так как квадрат числа не может быть отрицательным.
Таким образом, нужно рассмотреть два случая.
Первый случай:
Такую систему можно расписать в виде совокупности четырех систем. Запишем в виде краткого условия:
Из первого условия получим:
Из второго условия получим:
Таким образом, найдены решения:
Второй случай:
Последняя пара чисел не удовлетворяет условию о том, что решения должны быть составлены из неотрицательных чисел. Эта пара чисел не идет в ответ.
ответ:
Объяснение:
f(x) = x^2021 + a - заданная прямая функция.
f^(-1) (x) = корень 2021 степени из (x-a) - обратная функция.
Обратная функция имеет график, симметричный данному относительно прямой y = x.
Графики функции и обратной могут пересекаться только на прямой y = x.
Это значит, что функция сама должна пересекаться с прямой y = x.
Решаем уравнение и находим х при любом параметре а:
y = x^2021 + a = x
x = x^2021 + a
x^2021 - x + a = 0
Любой многочлен нечётной степени всегда имеет хотя бы один корень.
Поэтому при любом значении а будет хотя бы одно решение.
Преобразуем уравнение:
Если и
и 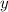 - целые числа, то и выражения
- целые числа, то и выражения  и
и 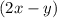 также являются целыми.
также являются целыми.
Тогда, выражения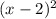 и
и 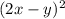 соответствуют квадратам целых чисел.
соответствуют квадратам целых чисел.
Если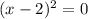 , то
, то 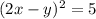 - но число 5 не является квадратом
- но число 5 не является квадратом 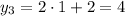
целого числа, поэтому этот вариант не реализуется.
Если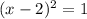 , то
, то 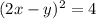 .
.
Если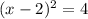 , то
, то 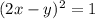 .
.
Если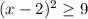 , то
, то 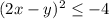 - эти варианты также не реализуются, так как квадрат числа не может быть отрицательным.
- эти варианты также не реализуются, так как квадрат числа не может быть отрицательным.
Таким образом, нужно рассмотреть два случая.
Первый случай:
Такую систему можно расписать в виде совокупности четырех систем. Запишем в виде краткого условия:
Из первого условия получим:
Из второго условия получим:
Таким образом, найдены решения:
Второй случай:
Из первого условия получим:
Из второго условия получим:
Таким образом, найдены решения:
Последняя пара чисел не удовлетворяет условию о том, что решения должны быть составлены из неотрицательных чисел. Эта пара чисел не идет в ответ.
ответ: