Имеем квадратное уравнение, где с - некоторое произвольное число (параметр), поэтому при разных значениях с уравнение может как иметь корни, так и не иметь. Поэтому нужно решить уравнения для всех возможных значений с.
Найдем дискриминант:
Рассмотрим 3 различных случая:
1) D < 0. Если D < 0, то уравнение не имеет решений. Найдем значения с, при которых дискриминант отрицателен: 64 - 8c < 0; 8c > 64 ⇔ c > 8. При таких значениях с корней у нас не будет вообще.
2) D = 0. Если D = 0, то уравнение имеет единственное решение: Найдем значение с, при котором дискриминант равен 0: 64 - 8c = 8 ⇔ c = 8. При таком значении параметра имеем один корень - х = 2.
3) D > 0. Если D > 0, то уравнение имеет два различных корня, которые находятся по общей формуле: . Выразим каждый из корней:
Аналогично
Найдем значения с, при которых дискриминант положителен: 64 - 8с > 0; 8с < 64 ⇔ c < 8. При таких значениях параметра у нас будут два корня:
ОТВЕТ: если с < 8, то если с = 8, то х = 2; если с > 8, то корней нет.
0,0(0 оценок)
Ответ:
02.08.2022 11:46
Скорость, км/ч t , ч S, км
х 180
х+(30:3) на 3 ч быстрее 180
.
30:3=10(км/ч) - на столько скорость второго больше
Объяснение: 2x²-8x+c = 0.
Имеем квадратное уравнение, где с - некоторое произвольное число (параметр), поэтому при разных значениях с уравнение может как иметь корни, так и не иметь. Поэтому нужно решить уравнения для всех возможных значений с.
Найдем дискриминант: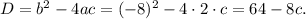
Рассмотрим 3 различных случая:
1) D < 0. Если D < 0, то уравнение не имеет решений. Найдем значения с, при которых дискриминант отрицателен: 64 - 8c < 0; 8c > 64 ⇔ c > 8. При таких значениях с корней у нас не будет вообще.
2) D = 0. Если D = 0, то уравнение имеет единственное решение: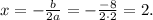 Найдем значение с, при котором дискриминант равен 0: 64 - 8c = 8 ⇔ c = 8. При таком значении параметра имеем один корень - х = 2.
Найдем значение с, при котором дискриминант равен 0: 64 - 8c = 8 ⇔ c = 8. При таком значении параметра имеем один корень - х = 2.
3) D > 0. Если D > 0, то уравнение имеет два различных корня, которые находятся по общей формуле: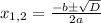 . Выразим каждый из корней:
. Выразим каждый из корней:
Аналогично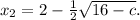
Найдем значения с, при которых дискриминант положителен: 64 - 8с > 0; 8с < 64 ⇔ c < 8. При таких значениях параметра у нас будут два корня: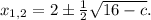
ОТВЕТ: если с < 8, то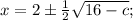 если с = 8, то х = 2; если с > 8, то корней нет.
если с = 8, то х = 2; если с > 8, то корней нет.
Скорость, км/ч t , ч S, км
х 180
х+(30:3) на 3 ч быстрее 180
.
30:3=10(км/ч) - на столько скорость второго больше
.
180/х - 180/(х+10)=3
180(х+10-х)=3х(х+10)
1800=3х²+30х
3х²+30х-1800=0
х²+10х-600=0
D/4=5²+600=625 (±25²)
х1= -5-25= - 30 -- не подходит решению
х2= -5+25=20 (км/ч) - скорость одного поезда
20+10=30(км/ч) - скорость другого