Алгебра: Решите систему неравенств:

ответ: Объяснение:Решить систему методом Крамера:Найдем главный определитель системы:где a, b, c - числовые коэффициенты при x, y, z соответственно.Найдем определитель разложением по первой строке:Δ = a₁ · (b₂c₃ - b₃c₂) - b₁ · (a₂c₃ - a₃c₂) + c₁ · (a₂b₃ - a₃b₂)Вычислим Δ:Δ ≠ 0 ⇒ система имеет единственное решение.Для нахождения корней необходимо вычислить еще три определителя:1. Δх.Заменим в главном определителе первый столбец на столбец свободных членов (d):Вычислим Δх:2. Δy.Заменим в главном...

Решите систему неравенств:

Показать ответ

Ответ:

egubiev

19.03.2023 21:48

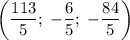
ответ: $\displaystyle \left(\frac{113}{5} ;\;-\frac{6}{5} ;\;-\frac{84}{5}\right)$

Объяснение:

Решить систему методом Крамера:

$\begin{equation*} \begin{cases} 2x+4y+3z=-10 \\-x+5y-2z=5 \\3x-2y+4z=3 \\ \end{cases}\end{equation*}$

Найдем главный определитель системы:

$\Delta=\begin{vmatrix} a_1& b_1&c_1\\ a_2 &b_2&c_2\\a_3& b_3&c_3\\\end{vmatrix}$

где a, b, c - числовые коэффициенты при x, y, z соответственно.

Найдем определитель разложением по первой строке:

Δ = a₁ · (b₂c₃ - b₃c₂) - b₁ · (a₂c₃ - a₃c₂) + c₁ · (a₂b₃ - a₃b₂)

Вычислим Δ:

$\displaystyle \Delta=\begin{vmatrix} 2& 4&3\\ -1 &5&-2\\3& -2&4\\\end{vmatrix}==2(5\cdot4-(-2)\cdot(-2))-4((-1)\cdot4-3\cdot(-2))+3((-1)\cdot(-2)-3\cdot5)==32-8-39=-15$

Δ ≠ 0 ⇒ система имеет единственное решение.

Для нахождения корней необходимо вычислить еще три определителя:

1. Δх.

Заменим в главном определителе первый столбец на столбец свободных членов (d):

$\Delta_x=\begin{vmatrix} d_1& b_1&c_1\\ d_2 &b_2&c_2\\d_3& b_3&c_3\\\end{vmatrix}$

Вычислим Δх:

$\displaystyle \Delta_x=\begin{vmatrix} -10& 4&3\\ 5 &5&-2\\3& -2&4\\\end{vmatrix}==-10\cdot(5\cdot4-(-2)\cdot(-2))-4\cdot(5\cdot4-3\cdot(-2))+3\cdot(5\cdot(-2)-3\cdot5)==-160-104-75=-339$

2. Δy.

Заменим в главном определителе второй столбец на столбец свободных членов (d):

$\Delta_y=\begin{vmatrix} a_1& d_1&c_1\\ a_2 &d_2&c_2\\a_3& d_3&c_3\\\end{vmatrix}$

Вычислим Δy:

$\displaystyle \Delta_y=\begin{vmatrix} 2& -10&3\\ -1 &5&-2\\3& 3&4\\\end{vmatrix}==2\cdot(5\cdot4-3\cdot(-2))+10\cdot((-1)\cdot4-3\cdot(-2))+3\cdot((-1)\cdot3-3\cdot5)==52+20-54=18$

3. Δz.

Заменим в главном определителе третий столбец на столбец свободных членов (d):

$\Delta_z=\begin{vmatrix} a_1& b_1&d_1\\ a_2 &b_2&d_2\\a_3& b_3&d_3\\\end{vmatrix}$

Вычислим Δz:

$\displaystyle \Delta_z=\begin{vmatrix} 2& 4&-10\\ -1 &5&5\\3& -2&3\\\end{vmatrix}==2\cdot(5\cdot3-(-2)\cdot5)-4\cdot((-1)\cdot3-3\cdot5)-10\cdot((-1)\cdot(-2)-3\cdot5)==50+72+130=252$

ответ рассчитывается по формулам:

$\displaystyle x=\frac{\Delta_x}{\Delta} ;\;\;\;\;\; y=\frac{\Delta_y}{\Delta} ;\;\;\;\;\; z=\frac{\Delta_z}{\Delta}$

Найдем корни:

$\displaystyle x=\frac{-339}{-15}=\frac{113}{5} ;\;\;\;\;\; y=\frac{18}{-15}=-\frac{6}{5} ;\;\;\;\;\; z=\frac{252}{-15}=-\frac{84}{5}$

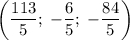
ответ: $\displaystyle \left(\frac{113}{5} ;\;-\frac{6}{5} ; \;-\frac{84}{5}\right)$

#SPJ1

0,0(0 оценок)

Ответ:

maria610

11.02.2022 12:01

Почему-то удалили мой ответ, пишу еще раз.
Формула суммы кубов
(3x+2)(9x^2-6x+4) = (3x)^3 + 2^3 = 27x^3 + 8
Подставляем
(27x^3 + 8)(3x + 4) = (3x - 4)^2 + 32
81x^4 + 24x + 108x^3 + 32 = 9x^2 - 24x + 16 + 32
81x^4 + 108x^3 - 9x^2 + 48x - 16 = 0
Корни у этого уравнения - иррациональные. Подберем примерно.
f(0) = -16 < 0
f(-1) = 81 - 108 - 9 - 48 - 16 = -100 < 0
f(-2) = 81*16 - 108*8 - 9*4 - 48*2 - 16 = 284 > 0
-2 < x1 < -1
f(1) = 81 + 108 - 9 + 48 - 16 = 212 > 0
0 < x2 < 1
Можно уточнить до 0,1
f(-1,6) = 81*1,6^4 - 108*1,6^3 - 9*1,6^2 - 48*1,6 - 16 = -27,37 < 0
f(-1,7) = 81*1,7^4 - 108*1,7^3 - 9*1,7^2 - 48*1,7 - 16 = 22,36 > 0
-1,7 < x1 < -1,6

f(0,3) = 81*0,3^4 + 108*0,3^3 - 9*0,3^2 + 48*0,3 - 16 = 1,16 > 0
f(0,2) = 81*0,2^4 + 108*0,2^3 - 9*0,2^2 + 48*0,2 - 16 = -5,77 < 0
0,2 < x2 < 0,3

Но я чувствую, что в задаче ошибка, потому что в 7 классе такое может быть только если на олимпиаде.

0,0(0 оценок)

Популярные вопросы: Алгебра