1 случай. 100 кг+50 кг=150 кг, в 150 кг содержится 28% кислоты , обозначим: p- доля кислоты в первом растворе q- доля кислоты во втором растворе 100·p-количество кислоты в первом растворе 50·q - количество кислоты во втором растворе выразим проценты в долях: 28%=(28/100)100% 28/100=7/25 - доля кислоты , после того, как смешали растворы. 150·7/25 количество кислоты после того, как смешали растворы. Напишем уравнение: 100p+50q=150·7/25 100p+50q=42 2 случай. Возьмем 50 кг из первого раствора и 50 кг второго раствора. 50 кг+50 кг =100 кг, в 100 кг содержится 36% кислоты 365 выразим в долях: 36%=(36/100)·100, 36/100=9/25 -доля кислоты, после того как смешали растворы. p- доля кислоты в первом растворе, q- доля кислоты во втором растворе. Напишем уравнение:50p+50q=100·9/25 50p+50q=36 Запишем систему: 100p+50q=42 50p+50q=36 Вычтем из первого уравнения второе, 50p=6 p=6/50=12/100=0,12 Подставим значение p в одно из уравнений: 50·0,12+50q=36 50q=36-6=30 50q=30 q=30/50=3/5=0,6 доля кислоты в первом растворе p=0,12, всего кислоты было 100 кг, следовательно кислоты в 100 кг раствора содержится 100·0,12=12 кг.
обозначим: p- доля кислоты в первом растворе
q- доля кислоты во втором растворе
100·p-количество кислоты в первом растворе
50·q - количество кислоты во втором растворе
выразим проценты в долях: 28%=(28/100)100%
28/100=7/25 - доля кислоты , после того, как смешали растворы.
150·7/25 количество кислоты после того, как смешали растворы.
Напишем уравнение: 100p+50q=150·7/25
100p+50q=42
2 случай. Возьмем 50 кг из первого раствора и 50 кг второго раствора.
50 кг+50 кг =100 кг, в 100 кг содержится 36% кислоты
365 выразим в долях: 36%=(36/100)·100, 36/100=9/25 -доля кислоты, после того как смешали растворы.
p- доля кислоты в первом растворе, q- доля кислоты во втором растворе.
Напишем уравнение:50p+50q=100·9/25
50p+50q=36
Запишем систему: 100p+50q=42
50p+50q=36 Вычтем из первого уравнения второе,
50p=6
p=6/50=12/100=0,12
Подставим значение p в одно из уравнений:
50·0,12+50q=36
50q=36-6=30
50q=30
q=30/50=3/5=0,6
доля кислоты в первом растворе p=0,12, всего кислоты было 100 кг,
следовательно кислоты в 100 кг раствора содержится 100·0,12=12 кг.
sin (5πx/9) = sin (πx/9) + sin (2πx/9)
sin (5πx/9) - sin (πx/9) = sin (2πx/9)
По формуле разности синусов:
2sin(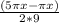
)cos(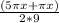
) - sin (2πx/9) = 0;
2 sin(2πx/9)cos(πx/3) - sin(2πx/9)=0;
sin (2πx/9) (2cos(πx/3)-1)=0;
sin (2πx/9)=0 или 2cos (πx/3)=1; cos (πx/3)=1/2
2πx/9=πn, n∈Z или πx/3=π/3+2πn, n∈Z или πx/3=-π/3+2πn, n∈Z;
Сокращаем на π:
2x/9=n, n∈Z или x/3=1/3+2n, n∈Z или x/3=-1/3+2n, n∈Z;
x=9n/2 или x=6n+1 или x=6n-1
Теперь отбираем корни уравнения, принадлежащие промежутку (4;8)
4<(9/2)n<8; 8/9<n<16/9; n=1, x=4,5
4<6n+1<8; 3<6n<7; 1/2<n<7/6; n=1; x=6+1=7;
4<6n-1<8; 5<6n<9; 5/6<n<3/2; n=1; x=6-1=5
ответ: x={4,5;5;7}