Решите систему уравнений методом постановки {15x-4y=8,{-3x+y=1.

Показать ответ

Ответ:

daniil6092002

03.03.2021 08:28

Объяснение:

I. График

а) при x≥0 IxI=x

y=(2x+2)/(x-1)=(2x-2+2+2)/(x-1)=2+4/(x-1)

этот график можно построить элементарными преобразованиями графика у=1/x

растянуть вдоль оси ОУ в 4 раза

сместить вправо на 1

переместить вверх на 2

ассимптоты у=2 ; х=1

б) при x<0 IxI=-x

y=(-2x+2)/(-x-1)=(-2x-2+2+2)/(-x-1)=2-4/(x+1)

этот график можно построить элементарными преобразованиями графика у=1/x

растянуть вдоль оси ОУ в 4 раза

отобразить симметрично относительно оси ОХ

сместить влево на 1

переместить вверх на 2

ассимптоты у=2 ; х=-1

II параметр

2IxI+2=aIxI-a

IxI(2-a)=-2-a

IxI=(-2-a)/(2-a)

IxI≥0

(-2-a)/(2-a)≥0

(2+a)/(2-a)≤0

решим методом интервалов

a=-2 ; a=2

в граничных точках ±2

проверим есть ли корни

а=2

(2IxI+2)/(IxI-1)=2

2IxI+2=2IxI-2

2=-2 нет корней

а=-2

(2IxI+2)/(IxI-1)=-2

2IxI+2=-2IxI+2

4IxI=0 x=0 есть корень

-------------------(-2)--------2--------------->

- + -

при a∈(-∞;-2]∪(2;+∞) уравнение имеет корни

тогда при a ∈(-2;2] уравнение не имеет корней

0,0(0 оценок)

Ответ:

bukinaleksandrp08nhi

23.06.2020 18:17

ответ: $d=40\ .$

Графиком квадратичной функции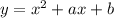 y=x^2+ax+b является парабола.

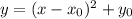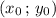Если необходимо начертить график этой параболы, то можно функцию представить в виде y=(x-x_0)^2+y_0 , где $(x_0\, ;\, y_0)$ - координаты вершины параболы. На координаты вершины будут влиять коэффициенты "а" и "b". Коэффициент перед 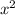x^2 влияет на степень сжатия параболы . В нашем случае он равен 1 .

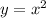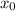И такую параболу можно начертить с переноса графика параболы y=x^2 на x_0 единиц вдоль оси ОХ вправо или влево в зависимости от знака числа 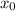x_0 , и на 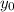y_0 вверх или вниз вдоль оси ОУ в зависимости от знака 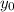y_0 . То есть парабола 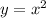y=x^2 только двигается вдоль осей координат .

На размеры параболы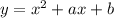 y=x^2+ax+b коэффициенты "а" и "b" не влияют. Они такие же, как и у параболы 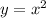y=x^2 . Поэтому вместо заданной параболы можно представить параболу 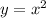y=x^2 с вершиной в точке О(0:0) .

Пары точек А,В и С, D симметричны относительно оси симметрии, которая проходит через вершину параболы . Осью симметрии параболы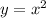 y=x^2 является ось ОУ . Если АВ=3 , а CD=13 , то точки В и D на параболе 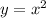y=x^2 имеют абсциссы, равные половине длин отрезков АВ и CD , то есть х(В)=3:2=1,5 , х(D)=13:2=6,5 .

Найдём ординаты этих точек, подставив абсциссы в уравнение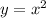 y=x^2 .

y(B)=1,5²=2,25 , y(D)=6,5²=42,25

Все точки на прямой АВ имеют ординаты, равные у=2,25 . Все точки на прямой CD имеют ординаты, равные у=42,25 . Поэтому расстояние между прямыми АВ и CD равно d=42,25-2,25=40 .

$\star \ \ x^2+ax+b=\Big(x+\dfrac{a}{2}\Big)^2-\dfrac{a^2}{4}+b\ \ \ \Rightarrow \ \ x_0=-\dfrac{a}{2}\ ,\ \ y_0=b-\dfrac{a^2}{4}\ \ \star\\\\\star \ \ x^2+ax+b=(x-x_0)^2+y_0=\Big(x+\dfrac{a}{2}\Big)^2-\dfrac{a^2}{4}+b\ \ \star$