Когда график пересекает ось абсцисс в какой-то точке, координаты этой точки (х;0), все точки лежащие на оси х имеют координату "ноль" по оси у. В итоге можем представить выражение следующим образом:
ответ: 1.
2)
Опять же в точке пересечения графика с абсциссой координаты по оси у это 0, значит:
ответ: 2 и -14.
3)
1) Можно раскрыть модуль по определению и увидеть, что получиться, а можно подумать. Есть какая-то функция, которая преобразует х в у (у=х), и отрицательные и положительные значения. А если взять модуль от х, то функция будет принимать те же значения для отрицательных значениях х, что и для положительных (когда они равны по модулю, пример -2 и 2), получается когда х будет отрицательным значения по оси х будут такими же, проще говоря всё чтобы справа (когда х положительный), отзеркалится влево по оси у. Покажу пример и другие графики внизу. То есть нам надо отразить график у=х как было сказано выше.
2) Тут уже по определению, но и всё просто:
Два линейных уравнения.
4)
Если что-то пересекается в одной точке на координатной плоскости, то у них есть общие точки, то есть существует такая точка M--> (x₀;y₀), которая подходит есть в любой из функций, которые пересекаются в этой точке.
Теперь построение на общей координатной плоскости
Первая функция: Получили точки пересечения с осью у и х соответственно.
Через исследование функции на экстремум. Производную возьмем Максимум и минимум функции достигается в точках, где производная равна 0. по т. Виета x1 = 1; x2 = -2. Единица в наш отрезок не попадает, значит, либо наибольшее, либо наименьшее значение будет в точке -2. Подставим -2 в исходное уравнение функции: В точке 1 значение функции примет минимальное: -3,5, но в наш отрезок эта точка не входит. Можно подставить точку -3, но там функция будет равняться 4,5. Значит, минимальное значение функция примет в точке 0. Функция там будет равняться нулю. Таким образом, сумма наибольшего и наименьшего значений на отрезке будет равняться 10+0=10
1)
Когда график пересекает ось абсцисс в какой-то точке, координаты этой точки (х;0), все точки лежащие на оси х имеют координату "ноль" по оси у. В итоге можем представить выражение следующим образом:
ответ: 1.
2)
Опять же в точке пересечения графика с абсциссой координаты по оси у это 0, значит: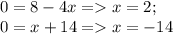
ответ: 2 и -14.
3)
1) Можно раскрыть модуль по определению и увидеть, что получиться, а можно подумать. Есть какая-то функция, которая преобразует х в у (у=х), и отрицательные и положительные значения. А если взять модуль от х, то функция будет принимать те же значения для отрицательных значениях х, что и для положительных (когда они равны по модулю, пример -2 и 2), получается когда х будет отрицательным значения по оси х будут такими же, проще говоря всё чтобы справа (когда х положительный), отзеркалится влево по оси у. Покажу пример и другие графики внизу. То есть нам надо отразить график у=х как было сказано выше.
2) Тут уже по определению, но и всё просто:
Два линейных уравнения.
4)
Если что-то пересекается в одной точке на координатной плоскости, то у них есть общие точки, то есть существует такая точка M--> (x₀;y₀), которая подходит есть в любой из функций, которые пересекаются в этой точке.
Теперь построение на общей координатной плоскости
Первая функция: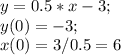
Получили точки пересечения с осью у и х соответственно.
Вторая функция: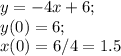
Третья функция: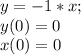
ответ: -1.
Производную возьмем
Максимум и минимум функции достигается в точках, где производная равна 0.
по т. Виета x1 = 1; x2 = -2.
Единица в наш отрезок не попадает, значит, либо наибольшее, либо наименьшее значение будет в точке -2.
Подставим -2 в исходное уравнение функции:
В точке 1 значение функции примет минимальное: -3,5, но в наш отрезок эта точка не входит. Можно подставить точку -3, но там функция будет равняться 4,5. Значит, минимальное значение функция примет в точке 0. Функция там будет равняться нулю. Таким образом, сумма наибольшего и наименьшего значений на отрезке будет равняться 10+0=10