Уточнение : десятичная периодическая дробь, как и конечная десятичная дробь, являются рациональными числами. Записать периодическую дробь можно в виде смешанного числа, либо в виде обыкновенной дроби, если целая часть равна нулю.
Чтобы записать периодическую дробь в виде смешанного числа, нужно оставить целую часть без изменения, а дробную часть периодической дроби, у которой период начинается сразу после запятой, записать в виде обыкновенной дроби, в которой числитель - это число из периода, а знаменатель содержит столько девяток, сколько цифр в периоде.
А)
Б)
В)
Г)
Д)
Е)
Если период равен нулю, то его можно просто отбросить, оставив число до периода : целое либо в виде конечной десятичной дроби.
Определите степень,старший коэффициент и свободный член многочлена
Степенью многочлена называют наибольшую из степеней входящих в него одночленов.
Значит нам нужно найти наибольшую степень при х
не буду вдаваться в объяснения как возводить многочлен в n-ную степень.. но есть правило, по которому, при возведении в степень первый и последний члены будут возводиться в ту степень в которую возводится весь многочлен
попробуем на конкретном примере
мы видим что наибольшая степень при х³⁴
старший коэффициент- это число стоящее перед х в наибольшей степени. В нашем случае это 3¹⁷
и свободный член это 1+1 ( 1 из первого слагаемого и 1 из второго слагаемого) =2
Уточнение : десятичная периодическая дробь, как и конечная десятичная дробь, являются рациональными числами. Записать периодическую дробь можно в виде смешанного числа, либо в виде обыкновенной дроби, если целая часть равна нулю.
Чтобы записать периодическую дробь в виде смешанного числа, нужно оставить целую часть без изменения, а дробную часть периодической дроби, у которой период начинается сразу после запятой, записать в виде обыкновенной дроби, в которой числитель - это число из периода, а знаменатель содержит столько девяток, сколько цифр в периоде.
А)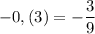
Б)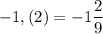
В)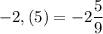
Г)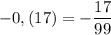
Д)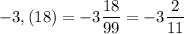
Е)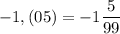
Если период равен нулю, то его можно просто отбросить, оставив число до периода : целое либо в виде конечной десятичной дроби.
Ж) 2,(0) = 2
З) -0,(0) = 0
И) 4,37(0) = 4,37
Степенью многочлена называют наибольшую из степеней входящих в него одночленов.
Значит нам нужно найти наибольшую степень при х
не буду вдаваться в объяснения как возводить многочлен в n-ную степень.. но есть правило, по которому, при возведении в степень первый и последний члены будут возводиться в ту степень в которую возводится весь многочлен
попробуем на конкретном примере
мы видим что наибольшая степень при х³⁴
старший коэффициент- это число стоящее перед х в наибольшей степени. В нашем случае это 3¹⁷
и свободный член это 1+1 ( 1 из первого слагаемого и 1 из второго слагаемого) =2