Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, а знаменатель первой умножить на числитель второй дроби:
2) Для постройки окружности на координатной прямой нужно уравнение:
;
где x; y - соответственные переменные; R - радиус.
При добавлении определённой точки в 1 четверти координатной плоскости, нужно вычесть координаты точки окружности(2;5); также у нас дан радиус 2.
Тем самым, мы получаем:
ответ:
3) Нарисовав треугольник на координатной плоскости, можно заметить, что у треугольник две стороны явно являются диагоналями прямоугольников 1x4. Так как прямоуголники равны, то и дагонали в них тоже равны => треугольник равнобедреный. (ч. и т. д.)
В решении.
Объяснение:
1. Выполнить деление:
(27 + b³)/(81 - b⁴) : (b² - 3b + 9)/(b² + 9);
1) Преобразовать первую дробь:
в числителе сумма кубов, разложить по формуле:
3³ + b³ = (3 + b)(3² - 3b + b²) =
= (3 + b)(9 - 3b + b²);
В знаменателе разность кубов, развернуть:
81 - b⁴ = (9 - b²)(9 + b²);
Преобразованная первая дробь:
(3 + b)(9 - 3b + b²)/(9 - b²)(9 + b²);
2) Произвести деление:
(3 + b)(9 - 3b + b²)/(9 - b²)(9 + b²) : (b² - 3b + 9)/(b² + 9) =
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, а знаменатель первой умножить на числитель второй дроби:
= [(3 + b)(9 - 3b + b²) * (b² + 9)] / [(9 - b²)(9 + b²) * (9 - 3b + b²)] =
сократить (разделить) (9 - 3b + b²) и (9 - 3b + b²) на (9 - 3b + b²), (b² + 9) и )(9 + b²) на (9 + b²):
= (3 + b)/(9 - b²)=
в знаменателе разность квадратов, развернуть:
= (3 + b)/(3 - b)(3 + b)=
сократить (разделить) (3 + b) и (3 + b) на (3 + b):
= 1/(3 - b). Последний ответ.
2. Избавиться от иррациональности в знаменателе.
5/(√11 - √6);
Нужно умножить дробь (числитель и знаменатель) на сопряжённое выражение (√11 + √6):
5/(√11 - √6) * (√11 + √6)/(√11 + √6) =
= [5 * (√11 + √6)] / [ (√11 - √6) * (√11 + √6)] =
в знаменателе развёрнута разность квадратов, свернуть:
= [5 * (√11 + √6)] / [(√11)² - (√6)²] =
= [5 * (√11 + √6)] / [11 - 6] =
= [5 * (√11 + √6)] / 5 =
сократить 5 и 5 =
= (√11 + √6). Последний ответ.
3. Найти значение выражения 39a-15b+25, если (3a-6b+4)/(6a-3b+4)=7.
1) Избавиться от дробного вида второго выражения:
(3a-6b+4)/(6a-3b+4)=7
3a-6b+4 = 7(6a-3b+4)
раскрыть скобки:
3a-6b+4 = 42a - 21b + 28
привести подобные члены:
3a-6b-42+21b = 28-4
-39a+15b=24/-1
39a-15b= -24;
2) Подставить в первое выражение значение второго выражения:
39a-15b+25;
39a-15b= -24;
-24 + 25 = 1.
1) Выведем y из этих функций:
5y = 1 - 9x
y = (1-9x) / 5
3y = 8 - 2x
y = (8 - 2x) / 3
Приводим равенства и решаем уравнение:
(1 - 9x) / 5 = (8 - 2x) / 3
3(1 - 9x) = 5(8 - 2x)
3 - 27x = 40 - 10x
-37 = 17x
x = - 37/17 => y = 54/85
ответ: ( -37/17; 54/85 ).
2) Для постройки окружности на координатной прямой нужно уравнение:
где x; y - соответственные переменные; R - радиус.
При добавлении определённой точки в 1 четверти координатной плоскости, нужно вычесть координаты точки окружности(2;5); также у нас дан радиус 2.
Тем самым, мы получаем:
ответ: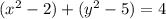
3) Нарисовав треугольник на координатной плоскости, можно заметить, что у треугольник две стороны явно являются диагоналями прямоугольников 1x4. Так как прямоуголники равны, то и дагонали в них тоже равны => треугольник равнобедреный. (ч. и т. д.)