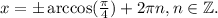Разберемся с правой частью. На множестве действительных чисел косинус принимает значения от -1 до 1 включительно, поэтому выражение должно попадать в данный промежуток значений. С учётом того, что , это возможно только при
(формально решаем неравенство , имеющее единственное целое решение - число 0, поскольку левая часть > -1, а правое < 1)
ОТВЕТ: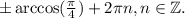
Используем формулы приведения:
Разделим обе части на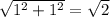 :
:
Разберемся с правой частью. На множестве действительных чисел косинус принимает значения от -1 до 1 включительно, поэтому выражение должно попадать в данный промежуток значений. С учётом того, что
должно попадать в данный промежуток значений. С учётом того, что 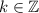 , это возможно только при
, это возможно только при 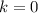
(формально решаем неравенство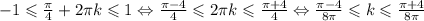 , имеющее единственное целое решение - число 0, поскольку левая часть > -1, а правое < 1)
, имеющее единственное целое решение - число 0, поскольку левая часть > -1, а правое < 1)
т.е. окончательно получаем, что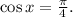
Отсюда