Оно, на первый взгляд, кажется очень сложным: здесь и шестая степень, и две неизвестные. Однако, как это всегда бывает, ответ всегда лежит на поверхности. Также и это уравнение можно легко решить, причем в данном случае x и y определены однозначно!
Для начала заметим, что .
Учитывая это перепишем уравнение:Теперь выполним хитрое преобразование:
Обращаем внимание на то, что равенство верно только, если , а .
Тогда решением исходного уравнения является пара чисел .
(см. объяснение)
Объяснение:
Рассмотрим уравнение:
Оно, на первый взгляд, кажется очень сложным: здесь и шестая степень, и две неизвестные. Однако, как это всегда бывает, ответ всегда лежит на поверхности. Также и это уравнение можно легко решить, причем в данном случае x и y определены однозначно!
Для начала заметим, что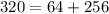 .
.
Учитывая это перепишем уравнение: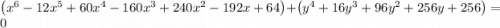 Теперь выполним хитрое преобразование:
Теперь выполним хитрое преобразование:
Обращаем внимание на то, что равенство верно только, если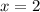 , а
, а 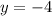 .
.
Тогда решением исходного уравнения является пара чисел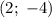 .
.
Уравнение решено!
х²+10х=39
х²+10х-39=0
k=b/2=10/2=5
D1=k²-ac=5²-1•(-39)=25+39=64
x1=-10-√64/1=-10-8/1=-18/1=-18
x2=-10+√64/1=-10+8/1=-2/1=-2
ответ: -18; -2.
х²+10х=56
х²+10х-56=0
k=b/2=10/2=5
D1=k²-ac=5²-1•(-56)=25+56=81
x1=-5-√81/1=-5-9/1=-14/1=-14
х²=-5+√81/1=-5+9/1=4/1=4
ответ: -14; 4.
(х/3+1)(х/4+1)=20
(х/3+1)(х/4+1)-20=0
(4х+12)(3х+12)-240=0 (привела к общему знаменателю, стала работать с числительным)
12х²+48х+36х+144-240=0
12х²+84х-96=0 |:12
х²+7х-8=0
D=b²-4ac=7²-4•1•(-8)=17
x1=-7-√17/1
x2=-7+√17/1
ответ: -7-√17/1; -7+√17/1.
25/9х²=100
25х²=900 |:25
х²=36
x=±√36
x1=-6; x2=6
ответ: -6; 6.
3х+4=х²
-х²+3х+4=0
х²-3х-4=0
По теореме, обратной теореме Виета:
х1=-1; х2=4
ответ: -1; 4.