Мы разложили левую часть на два множителя. Число 7 — простое, поэтому оно может раскладываться ровно на две пары целых множителей: (1; 7) и (–1, –7). Тогда получим четыре системы:
Первая система:
Вторая система:
Третья система:
Четвёртая система:
ответ: (3; –2), (–3; 2), (5; 2), (–5; –2).
P. S. Третью и четвёртую систему можно было бы не расписывать, если заметить, что при одновременной замене и значение выражения не изменится. Это означает, что если (x; y) является решением, то (–x; –y) тоже является решением.
Мы разложили левую часть на два множителя. Число 7 — простое, поэтому оно может раскладываться ровно на две пары целых множителей: (1; 7) и (–1, –7). Тогда получим четыре системы:
Первая система:
Вторая система:
Третья система:
Четвёртая система:
ответ: (3; –2), (–3; 2), (5; 2), (–5; –2).
P. S. Третью и четвёртую систему можно было бы не расписывать, если заметить, что при одновременной замене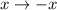
и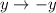 
значение выражения 
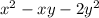не изменится. Это означает, что если (x; y) является решением, то (–x; –y) тоже является решением.
Почему я так смело возводил в квадрат? Если заметить ,то правая часть всегда неотрицательная ,а значит могу возводить и не наносить ограничения
Я привёл данную функцию к двум простейшим ,разберём их
Первая функция!
Мы знаем как выглядит модуль |2x+2| ,но мы его подняли ,а значит его вершина будет иметь координаты (-1;3)
Нам нужно одно решение с прямой x-a
Единственное решение может иметь только тогда ,когда прямая x-a касается вершины,то есть ,подставим вместо x=-1
Получаем:-1-a=3⇔-a=4⇔a=-4
Рассмотрим вторую функцию!
Если заметить ,то можно понять ,что вторая функция симметрична первой ,а значит её вершина будет иметь (-1;-3)
Делаем всё тоже самое ,подставляем x=-1
-1-a=-3⇔-a=-2⇔a=2
При а={-4;2} - будет единственное решение