Решаешь методом интервалов. 1. Ноль функции у=2х-7 при х=3.5 2. Ноль функции у=4-х при х=4 3. На промежутке от -бесконечности до 3.5 первая функция принимает отрицательное значение, вторая - положительное. Следовательно, неравенство на промежутке от -бесконечности до 3.5 (включительно) меньше или равно нулю, а значит отсюда необходимо включит только точку 3.5. 4. На промежутке от 3.5 до 4 первая функция принимает положительное значение, вторая - положительное. Следовательно, на данном промежутке неравенство больше или равно нулю, что удовлетворяет условию. НО точку 4 мы включить не можем (ОДЗ, на ноль делить нельзя). 5. На промежутке от 4 до +бесконечности первая функция принимает положительные значение, вторая - отрицательные, значит значение всего неравенства будет меньше или равно нулю. ответ: от 4 (включительно) до 3.5 (невключительно).
Тут разобрано два варианта, когда требуется найти вероятность, что "хотя бы три детали из пяти дефектные" и когда "ровно три детали из пяти дефектные".
Всего у нас изделий , изделий имеющих скрытый дефект .
Выбрать 5 изделий из 18 мы можем
Выбрать три дефектных, мы можем , остальные 2 можем выбрать
Вероятность события, равна отношению всех исходов к числу благоприятствующих исходов.
(хотя бы 3 из 5 - дефектные детали)
Если в задаче требуется найти вероятность, когда у нас ровно три дефектных изделия, то меняется только количество какими мы можем вытащить оставшиеся две детали, так как нам теперь не нужно учитывать дефектные. Теперь это будет
1. Ноль функции у=2х-7 при х=3.5
2. Ноль функции у=4-х при х=4
3. На промежутке от -бесконечности до 3.5 первая функция принимает отрицательное значение, вторая - положительное. Следовательно, неравенство на промежутке от -бесконечности до 3.5 (включительно) меньше или равно нулю, а значит отсюда необходимо включит только точку 3.5.
4. На промежутке от 3.5 до 4 первая функция принимает положительное значение, вторая - положительное. Следовательно, на данном промежутке неравенство больше или равно нулю, что удовлетворяет условию. НО точку 4 мы включить не можем (ОДЗ, на ноль делить нельзя).
5. На промежутке от 4 до +бесконечности первая функция принимает положительные значение, вторая - отрицательные, значит значение всего неравенства будет меньше или равно нулю.
ответ: от 4 (включительно) до 3.5 (невключительно).
Тут разобрано два варианта, когда требуется найти вероятность, что "хотя бы три детали из пяти дефектные" и когда "ровно три детали из пяти дефектные".
Всего у нас изделий , изделий имеющих скрытый дефект
, изделий имеющих скрытый дефект 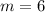 .
.
Выбрать 5 изделий из 18 мы можем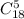
Выбрать три дефектных, мы можем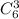 , остальные 2 можем выбрать
, остальные 2 можем выбрать 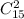
Вероятность события, равна отношению всех исходов к числу благоприятствующих исходов.
Если в задаче требуется найти вероятность, когда у нас ровно три дефектных изделия, то меняется только количество какими мы можем вытащить оставшиеся две детали, так как нам теперь не нужно учитывать дефектные. Теперь это будет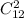
Соответственно: