на краях этого отрезка (x=-п/2 , x=п/2) cos x = 0 - Функция НЕинтегрируема
Б) [0 ; п ]
в середине этого отрезка (x=п/2) cos x = 0 - Функция НЕинтегрируема
В) [-п/4 ; 2п ]
внутри этого отрезка (x=п/2,x=3п/2,x=5п/2) cos x = 0 - Функция НЕинтегрируема
Г) [п/4 ; 2п]
внутри этого отрезка (x=п/2,x=3п/2,x=5п/2) cos x = 0 - Функция НЕинтегрируема
ответ: Функция НЕинтегрируема ни на каком отрезке.
Хотя, возможно, имеется в виду теорема о том, что
Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема на этом отрезке.
Формально под эту теорему подпадает случай А).
(Но что делать с границами отрезка? Если бы вместо отрезка был интервал (-п/2;п/2), то на этом интервале функция была бы интегрируема в любой точке, и вопросов бы не было и интеграл по интервалу можно было рассматривать, как предельные переходы к границам интервала.
Можно конечно, так же считать и для отрезка [-п/2;п/2], но это очень сомнительное допущение.)
Функция интегрируема, если cos x не равен нулю.
Функция неинтегрируема, если cos x =0.
cos x = 0 при x = п/2 + пk
Проверяем
A) [-п/2 ; п/2]
на краях этого отрезка (x=-п/2 , x=п/2) cos x = 0 - Функция НЕинтегрируема
Б) [0 ; п ]
в середине этого отрезка (x=п/2) cos x = 0 - Функция НЕинтегрируема
В) [-п/4 ; 2п ]
внутри этого отрезка (x=п/2,x=3п/2,x=5п/2) cos x = 0 - Функция НЕинтегрируема
Г) [п/4 ; 2п]
внутри этого отрезка (x=п/2,x=3п/2,x=5п/2) cos x = 0 - Функция НЕинтегрируема
ответ: Функция НЕинтегрируема ни на каком отрезке.
Хотя, возможно, имеется в виду теорема о том, что
Если функция f(x) непрерывна на отрезке [a,b], то она интегрируема на этом отрезке.
Формально под эту теорему подпадает случай А).
(Но что делать с границами отрезка? Если бы вместо отрезка был интервал (-п/2;п/2), то на этом интервале функция была бы интегрируема в любой точке, и вопросов бы не было и интеграл по интервалу можно было рассматривать, как предельные переходы к границам интервала.
Можно конечно, так же считать и для отрезка [-п/2;п/2], но это очень сомнительное допущение.)
Так что ответ может быть и А).
Интересная задача. Много преобразований, но легко решается.
Итак, приступим:
Начнем с "дано":
где t - время пути без задержки
где V - скорость без задержки.
Найти: V
Для начала напишем два уравнения
1)
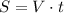- обычное уравнение пути =>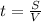 
2)
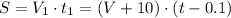
Подставим первое во второе, получим:
- тут начинается игра с буквами, раскрытие скобок, сокращения.
Записывать подробно не буду, напишу результат.
- получили обычное квадратное уравнение, которое решаем через дискриминант.
=>
Как видим, получили два корня уравнения -60 и 50.
Но, -60 не подходит по смыслу задачи.
То есть остается 50 км\ч, что и является ответом!
ответ: 50 км\ч