Алгебра: Решите уравнение: х2 – 3|х соч

Решите уравнение: х2 – 3|х соч

Показать ответ

Ответ:

AnastasiyaSm

06.02.2020 17:04

По определению,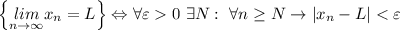 $\left\{\underset{n\rightarrow\infty}{lim}x_n=L\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n-L\right|$

Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение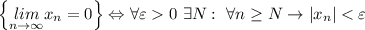 $\left\{\underset{n\rightarrow\infty}{lim}x_n=0\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n\right|$

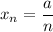
2) $x_n=\dfrac{a}{n}$

|x_n|

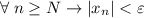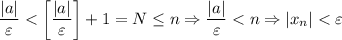
А значит, если взять $N=\left[\dfrac{|a|}{\varepsilon}\right] +1$ (*), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|a|}{\varepsilon}$

(*) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{|a|}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)

А это и означает, что предел данной последовательности равен 0

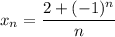
4) $x_n=\dfrac{2+(-1)^n}{n}$

|x_n|

$|2+(-1)^n|=\left\{\begin{array}{c}2-1=1,n=2k-1,k\in N \\2+1=3,n=2k,k\in N \end{array}\right. \Rightarrow |2+(-1)^n|\leq 3\; \forall n\in N$

А значит, если взять $N=\left[\dfrac{3}{\varepsilon}\right] +1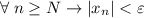$ (**), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|$

(**) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{3}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)

А это и означает, что предел данной последовательности равен 0

___________________________

2) a=1. Тогда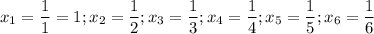 $x_1=\dfrac{1}{1}=1; x_2=\dfrac{1}{2}; x_3=\dfrac{1}{3}; x_4=\dfrac{1}{4}; x_5=\dfrac{1}{5}; x_6=\dfrac{1}{6}$

$x_1=\dfrac{2+(-1)^1}{1}=1;\;x_2=\dfrac{2+(-1)^2}{2}=1\dfrac{1}{2};\;x_3=\dfrac{2+(-1)^3}{3}=\dfrac{1}{3};\;x_4=\dfrac{2+(-1)^4}{4}=\dfrac{3}{4};\;x_5=\dfrac{2+(-1)^5}{5}=\dfrac{1}{5};\;x_6=\dfrac{2+(-1)^6}{6}=\dfrac{1}{2}.$

___________________________

Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x.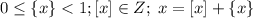 $0\leq \{x\}$

пример 2 и 4. Все теоремы и аксиомы, будьте добры, распишите. Действий, пусть и банальных, легких не

0,0(0 оценок)

Ответ:

Nottyt

05.10.2021 22:12

ответ: 6

Объяснение:

Применим следующий прием , не зависимо от того как , расположены заборы , все поле размером 80*80 можно дополнить некоторым количеством заборов , чтобы за забором был каждый участок размером 10*10 м .Чтобы это понять , нарисуйте в тетради в клетку квадрат 8 на 8 и замостите все место квадратами 2 на 2 и 1 на 4. Достаточно провести недостающие вертикали и горизонтали по клеточкам , чтобы каждый квадратик 1 на 1 был разделен забором.

Итак, допустим мы доложили до уже готовой конструкции заборы , чтобы каждый квадратик 10*10 был отделен . А теперь решили вновь убрать эти заборы , чтобы конструкция вернулась в первоначальное положение. Тогда внутри каждого квадрата 20*20 нужно убрать 4 забора размером 10 метров ( мысленно прочертили две горизонтальные и две вертикальные линии на стыках соседних не перпендикулярных заборов)

Внутри каждого прямоугольника 10*40 всего нужно убрать 3 забора размером 10 м ( так же мысленно прочертили недостающие линии) .

Теперь мысленно разобьем весь квадрат 80*80 на вертикальные и горизонтальные линии , расстояние между которыми 10 м.

Cколько линий получилось ? Правильно : 9 +9 =18 . Сколько квадратиков в 1 линии ? Правильно : 8

Пусть число участков 10*40 равно x , тогда число участков 20*20 равно 16-x.

Тогда учитывая ,что по краям острова заборов так же нет , то уравнение для суммарной длинны заборов выглядит так :

18*8*10 -3*x*10 -4*(16-x)*10 - 80*4 = 540

18*8 -3*x -4*(16-x)-32=54

x= 54+32+64 -144 = 150-144= 6

ответ : 6 участков 10*40

0,0(0 оценок)

Популярные вопросы: Алгебра