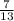1) a) Подставим значения точек в формулу и найдём p и q:
б) Вершину параболы(наименьшее значение, если коэффициент при x² положительный) можно найти по формуле: найдём q подставив точку (2;-5) в функцию:
2) График лежит выше оси абсцисс, когда отрицателен его дискриминант и коэффициент при x² положительный. У нас коэффициент положительный поэтому смотрим когда дискриминант отрицателен.
3) Подставим все значение в квадратичную функцию, общий вид которой y=ax²+bx+c, составим систему и найдём значения коэффициентов. {3=a·3²+b·3+c {3=a·(-1)²+b·(-1)+c {15=a·5²+b·5+c ↓ {3=9a+3b+c {3=a-b+c {15=25a+5b+c ↓от первого отнимем второе уравнение {3-3=9a-a+3b-(-b)+c-c {3=a-b+c {15=25a+5b+c ↓ {0=8a+4b {3=a-b+c {15=25a+5b+c ↓Выражаем b и c через а {b=-2a {c=3-3a {15=25a+5·(-2a)+(3-3а) ↓Отдельно решим 3 уравение 25a-10a-3a=15-3 12a=12 a=1 ↓Найдём b и c из первых двух уравнений b=-2·1=-2 c=3-3·1=0 Получаем квадратичную функцию: y=x²-2x
6) 6; 7) 13; 8) -1 ;9) см. об.; 10) если ответ нужно дать в числе, то у меня получилась дробь: -2 .
Объяснение:
1. 0*x=4. Любое число умножить на ноль будет ноль, а у нас оно равняется 4. Получается противоречие.
2. 6x - 1 = 5x. Переносим иксы влево, числа вправо (при переносе на другую сторону знак меняется на противоположный) и получаем уравнение вида: 6x - 5x = 1, упрощаем его: x = 1.
3. 7 - x = -18. Похожее на второе, но здесь можно переносить не иксы влево, числа вправо, а наоборот, тогда по-скольку мы перенесли их на другую сторону минус перед ним изменится на плюс и так будет легче работать: 7 + 18 = x, следовательно: x = 25.
4. Вначале нам потребуется раскрыть скобки: 5x - 7 + x = 4x - 9. А теперь классический перенос иксов и чисел: 5x - 4x + x = -2, далее:
2x = -2, x = -2 / 2, x = -1.
5. Записываем равенство в нужном нам виде:
(4a + 8) - (3 - 2a) = 23.
По-скольку минус перед скобками, все знаки в них меняются на противоположные: 4a + 8 - 3 + 2a = 23.
Упростим: 4a + 2a = 23 - 8 + 3, 6a = 18, a = 18/6 , a = 3.
a)
Подставим значения точек в формулу и найдём p и q:
б)
Вершину параболы(наименьшее значение, если коэффициент при x² положительный) можно найти по формуле:
найдём q подставив точку (2;-5) в функцию:
2)
График лежит выше оси абсцисс, когда отрицателен его дискриминант и коэффициент при x² положительный. У нас коэффициент положительный поэтому смотрим когда дискриминант отрицателен.
3)
Подставим все значение в квадратичную функцию, общий вид которой y=ax²+bx+c, составим систему и найдём значения коэффициентов.
{3=a·3²+b·3+c
{3=a·(-1)²+b·(-1)+c
{15=a·5²+b·5+c
↓
{3=9a+3b+c
{3=a-b+c
{15=25a+5b+c
↓от первого отнимем второе уравнение
{3-3=9a-a+3b-(-b)+c-c
{3=a-b+c
{15=25a+5b+c
↓
{0=8a+4b
{3=a-b+c
{15=25a+5b+c
↓Выражаем b и c через а
{b=-2a
{c=3-3a
{15=25a+5·(-2a)+(3-3а)
↓Отдельно решим 3 уравение
25a-10a-3a=15-3
12a=12
a=1
↓Найдём b и c из первых двух уравнений
b=-2·1=-2
c=3-3·1=0
Получаем квадратичную функцию:
y=x²-2x
ответ: 1) а; 2) в; 3) 25; 4) -1; 5) 3;
6) 6 ; 7) 13; 8) -1 ;9) см. об.; 10) если ответ нужно дать в числе, то у меня получилась дробь: -2
; 7) 13; 8) -1 ;9) см. об.; 10) если ответ нужно дать в числе, то у меня получилась дробь: -2 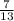 .
.
Объяснение:
1. 0*x=4. Любое число умножить на ноль будет ноль, а у нас оно равняется 4. Получается противоречие.
2. 6x - 1 = 5x. Переносим иксы влево, числа вправо (при переносе на другую сторону знак меняется на противоположный) и получаем уравнение вида: 6x - 5x = 1, упрощаем его: x = 1.
3. 7 - x = -18. Похожее на второе, но здесь можно переносить не иксы влево, числа вправо, а наоборот, тогда по-скольку мы перенесли их на другую сторону минус перед ним изменится на плюс и так будет легче работать: 7 + 18 = x, следовательно: x = 25.
4. Вначале нам потребуется раскрыть скобки: 5x - 7 + x = 4x - 9. А теперь классический перенос иксов и чисел: 5x - 4x + x = -2, далее:
2x = -2, x = -2 / 2, x = -1.
5. Записываем равенство в нужном нам виде:
(4a + 8) - (3 - 2a) = 23.
По-скольку минус перед скобками, все знаки в них меняются на противоположные: 4a + 8 - 3 + 2a = 23.
Упростим: 4a + 2a = 23 - 8 + 3, 6a = 18, a = 18/6 , a = 3.
6. (2x + 3)(4x - 3) - 17 = 2x(4x + 1). Раскрываем скобки и получаем:
8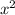 + 12x - 6x - 9 - 17 = 8
+ 12x - 6x - 9 - 17 = 8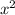 + 2x.
+ 2x.
8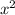 на обеих сторонах взаимоуничтожаются, и мы получаем следующее уравнение:
на обеих сторонах взаимоуничтожаются, и мы получаем следующее уравнение:
12x - 6x - 2x = 9 + 17
4x = 26.
x = 26 / 4, x = 6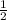
7. ( x + 1) / 2 - (2x - 1) / 3 = 3
Наименьшее общее кратное: 6
3 * (x + 1) / 6 - 2 * (x - 1) / 6 = 3
Убираем знаменатель и получаем:
3x + 3 - 2x + 2 = 3
(x + 5 )/6 = 3
x + 5 = 18
x = 13
8. 2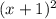 - (x - 3)(x + 3) = 7 +
- (x - 3)(x + 3) = 7 + 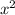 . Тут формулы сокращённого умножения.
. Тут формулы сокращённого умножения.
2 * (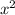 + 2x + 1) - (
+ 2x + 1) - (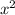 - 9) = 7 +
- 9) = 7 + 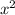 .
.
2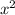 + 4x + 2 -
+ 4x + 2 - 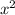 + 9 = 7 +
+ 9 = 7 + 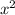 .
.
4x +2 + 9 = 7
4x = -4
x = -1.
9. Наименьшее общее кратное 12:
4(x - 3) / 3 + 3(3 / 4) = 3( 3x + 1) / 4 - (5x + 6) / 12.
(4x - 12 + 9 = 9x + 3 - (5x + 6)) / 12
4x - 12 + 9 = 9x + 3 - 5x - 6
4x - 9x + 5x = 12 + 3 - 6 - 9
упростив получается:
0x = 0, а любое число умножить на ноль будет ноль, так что любое число и подходит.
10. Выразив x в обоих уравнениях получаем:
x = (a - 4) / 5 и x = (3a + 5) / 2, если они равноправные, то приравниваем их:
(a - 4) / 5 = ( 3a - + 5) / 2
НСК: 10, поэтому:
2a - 8 = 15a + 25
13a = -33
a = -2