Условие можно переформулировать так: при каких значениях параметра двойное неравенство будет выполнено при для всех . Это гарантирует, что среди точек, удовлетворяющих системе, найдутся точки с любой абсциссой из и ординатой , что и является отрезком оси .
Итак, должна выполняться система: для всех . Для первого уравнения это равносильно тому, что наибольший корень трехчлена будет не меньше нуля, а наименьший -- не больше . Тогда это будет гарантировать то, что отрезок целиком попадет в параболу. Второе выполняется тогда и только тогда, когда (в противном случае является контрпримером). Получаем систему:
(Приводить здесь решение системы не стал, поскольку муторно и не относится к идейной составляющей).
Условие можно переформулировать так: при каких значениях параметра двойное неравенство
двойное неравенство 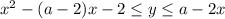 будет выполнено при
будет выполнено при  для всех
для всех ![x\in[-1,0]](/tpl/images/2102/1800/51327.png) . Это гарантирует, что среди точек, удовлетворяющих системе, найдутся точки с любой абсциссой из
. Это гарантирует, что среди точек, удовлетворяющих системе, найдутся точки с любой абсциссой из ![[-1,0]](/tpl/images/2102/1800/b0ace.png) и ординатой
и ординатой  , что и является отрезком
, что и является отрезком ![[-1,0]](/tpl/images/2102/1800/b0ace.png) оси
оси  .
.
Итак, должна выполняться система: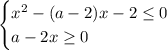 для всех
для всех ![x\in [-1,0]](/tpl/images/2102/1800/585c6.png) . Для первого уравнения это равносильно тому, что наибольший корень трехчлена будет не меньше нуля, а наименьший -- не больше
. Для первого уравнения это равносильно тому, что наибольший корень трехчлена будет не меньше нуля, а наименьший -- не больше 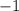 . Тогда это будет гарантировать то, что отрезок
. Тогда это будет гарантировать то, что отрезок ![[-1,0]](/tpl/images/2102/1800/b0ace.png) целиком попадет в параболу. Второе выполняется тогда и только тогда, когда
целиком попадет в параболу. Второе выполняется тогда и только тогда, когда 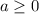 (в противном случае
(в противном случае 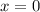 является контрпримером). Получаем систему:
является контрпримером). Получаем систему: ![\begin{cases}\dfrac{a-2+\sqrt{(a-2)^2+8}}{2}\geq 0\\\dfrac{a-2-\sqrt{(a-2)^2+8}}{2}\leq -1\\ a\geq 0\end{cases} \Leftrightarrow a\in [0,3]](/tpl/images/2102/1800/7e6bf.png)
(Приводить здесь решение системы не стал, поскольку муторно и не относится к идейной составляющей).