Уравнение однородное. Разделим его на косинус в квадрате. Это можно сделать, так как если cosx =0, то и sinx=0. что противоречит основному тригонометрическому тождеству.
Пусть tgx=t, тогда
Делаем обратную замену
tgx=1, x=
tgx=5, x=frctg5+
Уравнение однородное. Разделим его на косинус в квадрате. Это можно сделать, так как если cosx =0, то и sinx=0. что противоречит основному тригонометрическому тождеству.
Пусть tgx=t, тогда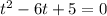
Делаем обратную замену
tgx=1, x=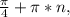
tgx=5, x=frctg5+