В решении.
Объяснение:
Доказать тождество.
1)2х²(4x²-3)(3+4х²)=32х⁶-18х²
2)3х²(2х²+5)(5-2х²)=75х³-12х⁷
Доказать тождество - значит преобразовать (решить) левую часть, если после преобразования обе части равны, тождество доказано.
В скобках развёрнута разность квадратов, свернуть:
2х² * (4x² - 3)(3 + 4х²) = 2х² * (4x² - 3)(4х² + 3) =
= 2х² * (16х⁴ - 9) = 32х⁶ - 18х² (левая часть).
32х⁶ - 18х² = 32х⁶ - 18х², тождество доказано.
3х² * (2х² + 5)(5 - 2х²) = 3х² * (5 + 2х²)(5 - 2х²) =
= 3х² * (25 - 4х⁴) = 75х² - 12х⁶ (левая часть).
75х² - 12х⁶ ≠ 75х³-12х⁷, выражение не является тождеством.
За интеграл я буду Июиспользовать вот этот знак:
1) Перепишите дробь:
2) Использовать свойства интегралов:
3) Вычислить интегралы и прибавить константу интегрирования С:
1) Найти неопределённый интеграл:
2) Упростить интеграл, используя метод замены переменной:
3) Преобразовать выражения:
4) Вычислить произведение:
5) Использовать свойство интегралов:
6) Вычислить интегралы:
7) Выполнить обратную замену:
8) Упростить выражение:
9) Вернуть пределы интегрирования и подставить в пример (8):
В решении.
Объяснение:
Доказать тождество.
1)2х²(4x²-3)(3+4х²)=32х⁶-18х²
2)3х²(2х²+5)(5-2х²)=75х³-12х⁷
Доказать тождество - значит преобразовать (решить) левую часть, если после преобразования обе части равны, тождество доказано.
1)2х²(4x²-3)(3+4х²)=32х⁶-18х²
В скобках развёрнута разность квадратов, свернуть:
2х² * (4x² - 3)(3 + 4х²) = 2х² * (4x² - 3)(4х² + 3) =
= 2х² * (16х⁴ - 9) = 32х⁶ - 18х² (левая часть).
32х⁶ - 18х² = 32х⁶ - 18х², тождество доказано.
2)3х²(2х²+5)(5-2х²)=75х³-12х⁷
В скобках развёрнута разность квадратов, свернуть:
3х² * (2х² + 5)(5 - 2х²) = 3х² * (5 + 2х²)(5 - 2х²) =
= 3х² * (25 - 4х⁴) = 75х² - 12х⁶ (левая часть).
75х² - 12х⁶ ≠ 75х³-12х⁷, выражение не является тождеством.
За интеграл я буду Июиспользовать вот этот знак:
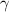
4 пример:1) Перепишите дробь:
2) Использовать свойства интегралов:
3) Вычислить интегралы и прибавить константу интегрирования С:
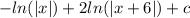
5 пример:1) Найти неопределённый интеграл:
2) Упростить интеграл, используя метод замены переменной:
3) Преобразовать выражения:
4) Вычислить произведение:
5) Использовать свойство интегралов:
6) Вычислить интегралы:
7) Выполнить обратную замену:
8) Упростить выражение:
9) Вернуть пределы интегрирования и подставить в пример (8):
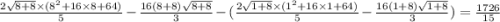
6 пример