32 см
Объяснение:
Пусть х см - ширина прямоугольника, тогда
(х+4) см - длина прямоугольника
(х(х+4)) кв.см -площадь прямоугольника
Т.к. по условиям задачи площадь равна 60 кв.см , составим и решим уравнение.
х(х+4)=60
х^2+4х=60
х^2+4х-60=0
а=1 b=4 c=-60
D=b^2-4ac=4^2-4*1*(-60)=16+240=256
x=(-b+корень D)/2а=(-4+корень 256)/2*1=(-4+16)/2=12/2=6
x=(-b-корень D)/2а=(-4-корень 256)/2*1=(-4-16)/2=-20/2=-10
-10 - значения стороны не может быть отрицательным
6 см-ширина прямоугольника
1) Находим периметр периметр по формуле 2*(a+b)=2*(6+(6+4))=32 см
n^2 - это число во второй степени
а - длина прямоугольника
b - ширина прямоугольника
а - ? см, на 4 см >, чем b
b - ? см
S=60 см²
Р - ? см
подставим известные величины
перенесём всё в левую часть и приравняем уравнение к нулю, при этом не забываем сменить знак на противоположный
Квадратное уравнение имеет вид:
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
не удовлетворяет условию задачи, так как сторона прямоугольника не может быть отрицательной
следовательно (см) - ширина прямоугольника.
(см) - длина прямоугольника.
(см)
ответ: 32 см периметр прямоугольника.
32 см
Объяснение:
Пусть х см - ширина прямоугольника, тогда
(х+4) см - длина прямоугольника
(х(х+4)) кв.см -площадь прямоугольника
Т.к. по условиям задачи площадь равна 60 кв.см , составим и решим уравнение.
х(х+4)=60
х^2+4х=60
х^2+4х-60=0
а=1 b=4 c=-60
D=b^2-4ac=4^2-4*1*(-60)=16+240=256
x=(-b+корень D)/2а=(-4+корень 256)/2*1=(-4+16)/2=12/2=6
x=(-b-корень D)/2а=(-4-корень 256)/2*1=(-4-16)/2=-20/2=-10
-10 - значения стороны не может быть отрицательным
6 см-ширина прямоугольника
1) Находим периметр периметр по формуле 2*(a+b)=2*(6+(6+4))=32 см
n^2 - это число во второй степени
а - длина прямоугольника
b - ширина прямоугольника
а - ? см, на 4 см >, чем b
b - ? см
S=60 см²
Р - ? см
подставим известные величины
перенесём всё в левую часть и приравняем уравнение к нулю, при этом не забываем сменить знак на противоположный
Квадратное уравнение имеет вид: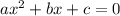
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
не удовлетворяет условию задачи, так как сторона прямоугольника не может быть отрицательной
следовательно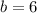 (см) - ширина прямоугольника.
(см) - ширина прямоугольника.
ответ: 32 см периметр прямоугольника.