Алгебра: Решите уравнение в действительных числах:

Решите уравнение в действительных числах:

x^5-5x^3+5x-4=0

Показать ответ

Ответ:

madama1994

16.08.2021 23:03

$\sqrt[5]{2-\sqrt{3}}+\sqrt[5]{2+\sqrt{3}}$

Объяснение:

Представим левую часть в несколько ином виде. Рассмотрим выражение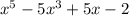 x^5-5x^3+5x-2 . Заметим, что при x = 2 значение выражения равно нулю. Значит, выражение можно представить в виде произведения многочлена 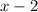x-2 и многочлена 4-ой степени. Поделив в столбик

Исходное уравнение можно представить, как

(x-2)(x^2+x-1)^2-2=0

При x ≤ 2 левая часть не превосходит -2, так как квадрат всегда неотрицателен, а x-2 ≤ 0. Значит, уравнение может иметь корни только при x > 2. Тогда корень уравнения можно представить в виде суммы двух взаимно обратных чисел (такая сумма по модулю не меньше двух).

Пусть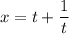 $x=t+\dfrac{1}{t}$ . Тогда

$\left(t+\dfrac{1}{t}-2\right)\left(\left(t+\dfrac{1}{t}\right)^2+t+\dfrac{1}{t}-1\right)^2-2=0\\\dfrac{t^2-2t+1}{t}\cdot\left(\dfrac{t^4+t^3+t^2+t+1}{t^2}\right)^2-2=0\\\dfrac{(t-1)^2}{t}\cdot\left(\dfrac{t^5-1}{(t-1)t^2}\right)^2-2=0\\\dfrac{(t-1)^2}{t}\cdot\dfrac{t^{10}-2t^5+1}{(t-1)^2t^4}-2=0$

При t = 1 x = 2, что противоречит условию x > 2. Значит, на (t-1)² можно сократить:

$\dfrac{t^{10}-2t^5+1}{t^5}-2=0\\t^5+\dfrac{1}{t^5}-4=0$

Пусть t^5=z :

$z+\dfrac{1}{z}-4=0\\\dfrac{z^2-4z+1}{z}=0$

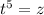Решим квадратное уравнение в числителе:

$D_{/4}=2^2-1=3\\z=2\pm\sqrt{3}\\t=\sqrt[5]{2\pm\sqrt{3}} \\x=\sqrt[5]{2\pm\sqrt{3}} +\dfrac{1}{\sqrt[5]{2\pm\sqrt{3}} }=\sqrt[5]{2\pm\sqrt{3}} +\dfrac{\sqrt[5]{2\mp\sqrt{3}} }{\sqrt[5]{2\pm\sqrt{3}}\cdot\sqrt[5]{2\mp\sqrt{3}} }=\\=\sqrt[5]{2\pm\sqrt{3}} +\sqrt[5]{2\mp\sqrt{3}}$

Оба корня можно представить как один, так как по факту это просто слагаемые, переставленные местами. Получаем $x=\sqrt[5]{2+\sqrt{3}} +\sqrt[5]{2-\sqrt{3}}$