1) ( 14y+21) ( 1,8-0,3y)=0
Делим ур-ние на 2 части:
14у+21=0 и 1.8-0.3у=0
14у=0-21 0,3у=1,8
14у=-21 у=1,8/0,3
у=6
у=-21/14
у=-1,5
ответ:-1,5;6.
2) 2( 4x+1)-x+7x+3
Чтобы решить данное уравнение нужно:
1. Раскрыть скобки.
Чтобы раскрыть скобки перед которыми стоит число нужно данное число умножить на каждое число со скобок.
2. Записать слагаемые с переменной в левой части уравнения, а свободные слагаемые в правой части уравнения.
При переносе слагаемых с одной части уравнения во вторую, нужно знаки сменить на противоположные.
3. Свести подобные слагаемые.
4. Найти значение переменной.
2 * 4х + 2 * 1 - х = 7х + 3;
8х + 2 - х = 7х + 3;
8х - х - 7х = 3 - 2;
0х = 1.
ответ: уравнение не имеет решений, так как на ноль делить нельзя.
Первое задание
Сделаем замену , при этом . Получим уравнение:
Тут по теореме Виета сразу видно, что первый корень равен единице. Тогда второй корень равен –9.
Вернёмся к исходной переменной:
ответ: одно решение.
Второе задание
Основания степеней больше единицы, поэтому, переходя к неравенству показателйе, знак сохранится:
Приравняем левую часть выражения к нулю, решим через дискриминант и разложим на множители:
Применив метод интервалов, получим, что . Поскольку неравенство строгое, имеем два целых решения: –1 и 0.
ответ: два решения.
Третье задание
ОДЗ:
Или
Или (ведь речь о целых числах).
Теперь решим уравнение:
Решений было бы бесконечное количество, если бы не ОДЗ: под него подпадают только числа –1, 0, 1, 2 (то есть четыре штуки).
ответ: четыре решения.
Четвёртое задание
Основание логарифма больше единицы, поэтому при переходе к неравенству выражений под логарифмом знак сохранится:
Решений было бы бесконечное количество, но с учётом ОДЗ получим: . Здесь решениями будут числа –1, 0, 1, 2, 3.
ответ: пять решений.
1) ( 14y+21) ( 1,8-0,3y)=0
Делим ур-ние на 2 части:
14у+21=0 и 1.8-0.3у=0
14у=0-21 0,3у=1,8
14у=-21 у=1,8/0,3
у=6
у=-21/14
у=-1,5
ответ:-1,5;6.
2) 2( 4x+1)-x+7x+3
Чтобы решить данное уравнение нужно:
1. Раскрыть скобки.
Чтобы раскрыть скобки перед которыми стоит число нужно данное число умножить на каждое число со скобок.
2. Записать слагаемые с переменной в левой части уравнения, а свободные слагаемые в правой части уравнения.
При переносе слагаемых с одной части уравнения во вторую, нужно знаки сменить на противоположные.
3. Свести подобные слагаемые.
4. Найти значение переменной.
2 * 4х + 2 * 1 - х = 7х + 3;
8х + 2 - х = 7х + 3;
8х - х - 7х = 3 - 2;
0х = 1.
ответ: уравнение не имеет решений, так как на ноль делить нельзя.
Первое задание
Сделаем замену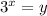
, при этом 
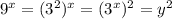. Получим уравнение:
Тут по теореме Виета сразу видно, что первый корень равен единице. Тогда второй корень равен –9.
Вернёмся к исходной переменной:
ответ: одно решение.
Второе задание
Основания степеней больше единицы, поэтому, переходя к неравенству показателйе, знак сохранится:
Приравняем левую часть выражения к нулю, решим через дискриминант и разложим на множители:
Применив метод интервалов, получим, что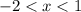
. Поскольку неравенство строгое, имеем два целых решения: –1 и 0.
ответ: два решения.
Третье задание
ОДЗ:
Или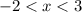
Или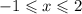
(ведь речь о целых числах).
Теперь решим уравнение:
Решений было бы бесконечное количество, если бы не ОДЗ: под него подпадают только числа –1, 0, 1, 2 (то есть четыре штуки).
ответ: четыре решения.
Четвёртое задание
ОДЗ:
Основание логарифма больше единицы, поэтому при переходе к неравенству выражений под логарифмом знак сохранится:
Решений было бы бесконечное количество, но с учётом ОДЗ получим: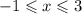
. Здесь решениями будут числа –1, 0, 1, 2, 3.
ответ: пять решений.