Решите уравнения 2х - (6х + 1) = 9 4х - (7х - 2) = 17 4 - 2(х+3)=4(х - 5) 5х - (7х + 7) = 9 3у - (5 - у) = 11 5х+3 =7х - 5(2х+1) 2х - (6х - 5) = 45 (6х+1)-(3 -2х) = 14 9 - (8х - 11) = 12 с - 32 = -7(с + 8) 3(4х - 8) = 3х - 6 5(х - 7) = 3(х - 4) - 4(-х + 7) = х + 17 4(х -3) -16 = 5(х-5) 8(2α - 6)=2(4α + 3) -4(3 - 5х) = 18х - 7 6α + (3α - 2) = 14 8х - (7х - 142) = 51 2х+7=3х - 2(3х - 1) -5·(3а+1)-11=-16, -3,2n+4,8=-2·(1,2n+2,4) -4·(-к+7)=к+17 -5·(0,8t-1,2)=-t+7,2 -5·(0,8f-1,4)=-f+7 1,2-2·(1,3y+1)=5,6y-27,04 6·(2c-3)+2·(4-3c)=5 4·(x-3)-16=5·(x-5) -3·(2,1m-1)+4,8=-6,7m+9,4 8-7·(c-2)=2·(2c-3)+3c -4·(3-5z)=18z-7 5·(y-3)+27=4y+3·(2y-5) 5·(r-7)=3·(r-4)-27 8·(2f-6)=2·(4f+3),

Объяснение:

1)x4 + 13x2 + 36 = 0

Сделаем замену y = x2, тогда биквадратное уравнение примет вид

y2 + 13y + 36 = 0

Для решения этого квадратного уравнения найдем дискриминант:

D = b2 - 4ac = 132 - 4·1·36 = 169 - 144 = 25

y1 =  -13 - √25  =  -9

2·1

y2 =  -13 + √25  =  -4

2·1

x2 =  -9

x2 =  -4

2)25x4 + 16x2 + 9 = 0

Сделаем замену y = x2, тогда биквадратное уравнение примет вид

25y2 + 16y + 9 = 0

Для решения этого квадратного уравнения найдем дискриминант:

D = b2 - 4ac = 162 - 4·25·9 = 256 - 900 = -644

ответ: так как дискриминант меньше нуля то корней нет

Иррациональное

Решение

:

1)x+5=0

x+(5-5)= -5

x= -5

2) x=     _ 1

               5

Сам график не построю, но всё, что нужно для его построения, напишу

Сначала нужно выразить одну переменную через другую:

y - 6x = -25

y = 6x - 25

-y - x = -5

y = 5 - x

Данные функции являются линейными, поэтому их графиками будут прямые, для построения графиков этих функций нужно подставить значение x, и найти при данном значении x значение y (Т.е., к примеру в первой функции при x = 1, y = 6 * 1 - 25 = -19):

y = 6x - 25

Координаты:

x = 1   y = -19

x = 0   y = -25

Координаты найдены, теперь для построения графика нужно отметить точки, соответствующие данным координатам на координатной плоскости, соединить их и вывести прямую за пределы этих точек

То же самое делаешь и со второй функцией:

y = 5 - x

Координаты:

x = 0   y = 5

x = 1   y = 4

Координаты найдены, теперь для построения графика нужно отметить точки, соответствующие данным координатам на координатной плоскости, соединить их и вывести прямую за пределы этих точек

Данные прямые пересекутся, и точка их пересечения будет решением системы уравнений

ответом будет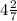 и

В связи с таким ответом вопрос: ты точно всё правильно написал?