1) графический. Нужно найти для каждого уравнения 2 корня, построить 2 прямые, где они пересекутся это и будет решение системы уравнения. 2) Метод подстановки 1) Выразим х через у из первого уравнения системы: х = 5 - 3у.
2)Подставим полученное выражение вместо х во второе уравнение системы: (5 - 3у) у — 2. 3)Решим полученное уравнение:
4) Подставим поочередно каждое из найденных значений у в формулу х = 5 - Зу. Если то 5) Пары (2; 1) и решения заданной системы уравнений.
ответ: (2; 1) 3)Алгебраическое сложение. Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения:
Вычтем второе уравнение системы из ее первого уравнения:
В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой:
Эту систему можно решить методом подстановки. Из второго уравнения находим Подставив это выражение вместо у в первое уравнение системы, получим
Осталось подставить найденные значения х в формулу
Объяснение:
1) Приводишь к общему знаменателю и при этом выполняется:
6х - 1 ≠ 0
х ≠ 1/6
(x+2)(6x-1) = 15
6x^2-x+12x-2-15 = 0
6x^2+11x-17 = 0
D = b^2-4ac
D = 11^2-4*6*(-17) = 121+408 = 529
x1 = (-b+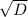 )/2a = (-11+23)/2*6 = 12/12 = 1
)/2a = (-11+23)/2*6 = 12/12 = 1
x2 = (-b-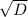 )/2a = (-11-23)/2*6 = -34/12 = -17/6
)/2a = (-11-23)/2*6 = -34/12 = -17/6
ответ: 1; -17/6
2) Чтобы найти точку пересечения двух графиков достаточно их приравнять и решить уравнение, т.е.:
2/x = x-1
2/x - x + 1 = 0
-x^2+x+2 = 0 Домножим на (-1):
x^2 -x -2 =0
по т. Виета:
x1+x2 = 1
x1*x2 = -2
x1= 2 x2= -1
Если x = 2, то у = 1
Если х = -1, то у = -2
ответ: (2;1) и (-1;-2)
2) Метод подстановки 1) Выразим х через у из первого уравнения системы: х = 5 - 3у.
2)Подставим полученное выражение вместо х во второе уравнение системы: (5 - 3у) у — 2.
3)Решим полученное уравнение:
4) Подставим поочередно каждое из найденных значений у в формулу х = 5 - Зу. Если то
5) Пары (2; 1) и решения заданной системы уравнений.
ответ: (2; 1)
3)Алгебраическое сложение. Умножим все члены первого уравнения системы на 3, а второе уравнение оставим без изменения:
Вычтем второе уравнение системы из ее первого уравнения:
В результате алгебраического сложения двух уравнений исходной системы получилось уравнение, более простое, чем первое и второе уравнения заданной системы. Этим более простым уравнением мы имеем право заменить любое уравнение заданной системы, например второе. Тогда заданная система уравнений заменится более простой системой:
Эту систему можно решить методом подстановки. Из второго уравнения находим Подставив это выражение вместо у в первое уравнение системы, получим
Осталось подставить найденные значения х в формулу
Если х = 2, то
Таким образом, мы нашли два решения системы: