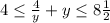Решите уравнения:
а) [4x-1]<9;
б) [7x+13]>8:
Очень нужно

Пацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезнуюПацанам привет остальным соболезную

Объяснение:

1. -15 ≤ 1-2у ≤ 0

2.

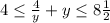
Объяснение:

1. Т.к. в линейном выражении 1-2у перед у стоит знак "-", то при вычислении пределов возможных значений нужно либо поменять направление знаков больше (меньше) либо поменять местами подставляемые значения 1/2 и 8.

для 1/2 ≤ у: 1-2у ≤ 0

для у ≤ 8:  1-2у ≥ -15

Тогда: -15 ≤ 1-2у ≤ 0

2. Здесь перед у знак "+", но появилась нелинейная зависимость 4/у, поэтому нужно вычислить производную функции (4/у + у) и приравнять её к нулю, чтобы найти ее экстремум.

Но так как значение -2 не попадает в наш промежуток по условию, то это значение отбрасываем.

Значит, в точке у=2 имеем экстремум. Определим  его значение:

для у=2: .

На остальных участках функция либо возрастает, либо убывает. подставим граничные значения из условия:

для у=1/2 :

для у=8: .

Т.е. имеем кривую с максимумами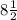 и минимумом 4.

Тогда