1) Отдельно разложим на множители 2 и 3 -ий знаменатели:
x^2 + x - 2 = (x+2)(x-1)
x^3+2x^2-x-2 = (x+2)(x^2 - 1) Итак ОДЗ: х не равен +-1;-2
Домножив на общий знаменатель , получим следующее уравнение 3-й степени:
2x^3 + x^2 - 7x - 6 = 0 Подбором находим один корень: х1 = -1( не входит в ОДЗ)
Разделив многочлен на (х+1) получим в частном:2x^2 - x - 6
2x^2 - x - 6 = 0 D = 49
x2 = (1+7)/4 = 2
x3 = (1-7)/4 = -1,5
ответ: -1,5; 2.
2)Сгруппируем множители:
[(x-3)(x+2)] * [(x-2)(x+1)] = 5
(x^2-x-6)(x^2-x-2) = 5
Обозначим: (x^2-x-2) = t
(t-4)t = 5
t^2 - 4t - 5 = 0
t1 = -1 t2 = 5
x^2-x-2=-1 x^2-x-2=5
x^2-x-1 =0 x^2 -x-7=0
x(1;2) = (1+-кор5)/2 х(3;4) = (1+-кор29)/2
ответ:x(1;2) = (1+-кор5)/2 х(3;4) = (1+-кор29)/2
3) кор[(x-2)(x+2)] - кор[(x-2)(x+1)] = кор[(x-2)(x-3)] ОДЗ:(-беск; -2];2;[3;беск)
Cразу находим первый корень: х1 = 2.
Пусть теперь х не= 2.
Поделим все уравнение на кор(х-2):
кор(х+2) - кор(х+1) = кор(х-3)
Возводим в квадрат:
2х+3-2кор[(x+2)(x+1)] = x-3
2кор[(x+2)(x+1)] = x+6
4(x+2)(x+1) = x^2 + 12x + 36
3x^2 = 28 x^2 = 28/3 x2 = -кор(28/3) x3 = кор(28/3) входят в ОДЗ
ответ: 2; -кор(28/3); кор(28/3).
4) x^2(x+4)^2 + 16x^2 = 8(x+4)^2 + 10x^2(x+4)
Допишу потом в сообщении...нет больше времени..
Решение пунктов 1 и 2, предложенное vajny, - правильные
( поэтому не буду повторяться),
но в пункте 3 - корень x2 = -кор(28/3)
не удовлетворяет равенству
( под знаком корня - отрицательные значения ),
поэтому корень x2 = -кор(28/3) - лишний и должен быть отброшен.
Остальные корни пункта 3 - верные.
Решение пункта 4.
Исходное выражение может быть приведено к следующему:
(
Надо найти корни выражений в скобках в числителе.
Корни уравнения
x1= 2*кор(5)+2; x2=2-2*кор(5); ( это и есть решение)
Дискриминант выражения
равен минус 28, поэтому выражение не имеет действительных корней.
1) Отдельно разложим на множители 2 и 3 -ий знаменатели:
x^2 + x - 2 = (x+2)(x-1)
x^3+2x^2-x-2 = (x+2)(x^2 - 1) Итак ОДЗ: х не равен +-1;-2
Домножив на общий знаменатель , получим следующее уравнение 3-й степени:
2x^3 + x^2 - 7x - 6 = 0 Подбором находим один корень: х1 = -1( не входит в ОДЗ)
Разделив многочлен на (х+1) получим в частном:2x^2 - x - 6
2x^2 - x - 6 = 0 D = 49
x2 = (1+7)/4 = 2
x3 = (1-7)/4 = -1,5
ответ: -1,5; 2.
2)Сгруппируем множители:
[(x-3)(x+2)] * [(x-2)(x+1)] = 5
(x^2-x-6)(x^2-x-2) = 5
Обозначим: (x^2-x-2) = t
(t-4)t = 5
t^2 - 4t - 5 = 0
t1 = -1 t2 = 5
x^2-x-2=-1 x^2-x-2=5
x^2-x-1 =0 x^2 -x-7=0
x(1;2) = (1+-кор5)/2 х(3;4) = (1+-кор29)/2
ответ:x(1;2) = (1+-кор5)/2 х(3;4) = (1+-кор29)/2
3) кор[(x-2)(x+2)] - кор[(x-2)(x+1)] = кор[(x-2)(x-3)] ОДЗ:(-беск; -2];2;[3;беск)
Cразу находим первый корень: х1 = 2.
Пусть теперь х не= 2.
Поделим все уравнение на кор(х-2):
кор(х+2) - кор(х+1) = кор(х-3)
Возводим в квадрат:
2х+3-2кор[(x+2)(x+1)] = x-3
2кор[(x+2)(x+1)] = x+6
4(x+2)(x+1) = x^2 + 12x + 36
3x^2 = 28 x^2 = 28/3 x2 = -кор(28/3) x3 = кор(28/3) входят в ОДЗ
ответ: 2; -кор(28/3); кор(28/3).
4) x^2(x+4)^2 + 16x^2 = 8(x+4)^2 + 10x^2(x+4)
Допишу потом в сообщении...нет больше времени..
Решение пунктов 1 и 2, предложенное vajny, - правильные
( поэтому не буду повторяться),
но в пункте 3 - корень x2 = -кор(28/3)
не удовлетворяет равенству
кор(х+2) - кор(х+1) = кор(х-3)
( под знаком корня - отрицательные значения ),
поэтому корень x2 = -кор(28/3) - лишний и должен быть отброшен.
Остальные корни пункта 3 - верные.
Решение пункта 4.
Исходное выражение может быть приведено к следующему:
(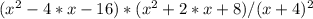
Надо найти корни выражений в скобках в числителе.
Корни уравнения
x1= 2*кор(5)+2; x2=2-2*кор(5); ( это и есть решение)
Дискриминант выражения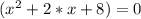
равен минус 28, поэтому выражение не имеет действительных корней.