Хорошо, давайте решим это уравнение в целых числах.
Пошаговое решение:
1. Для начала, перенесем все члены уравнения на одну сторону:
xy + 4x - 2y - 7 - 4 = 0
xy + 4x - 2y - 11 = 0
2. Заметим, что в уравнении есть два переменных: x и y. Нам нужно выразить одну из переменных через другую. Давайте попробуем выразить x через y.
Для этого мы приведем уравнение к виду: x = выражение относительно y.
3. Для начала, выделим общие множители в первых двух членах уравнения:
x(y + 4) - 2y - 11 = 0
4. Теперь, выразим x через y, разделив обе части уравнения на (y + 4):
x = (2y + 11) / (y + 4)
5. Итак, мы нашли выражение для x через y.
Таким образом, решение уравнения xy + 4x - 2y - 7 = 4 в целых числах выглядит следующим образом:
x = (2y + 11) / (y + 4).
Пояснение: Мы использовали метод алгебраических преобразований, чтобы перенести все члены уравнения на одну сторону, чтобы получить выражение для x через y. Это позволяет нам найти значения x и y, удовлетворяющие уравнению.
(3; –1), (5; –3), (1; –7), (–1; –5)
Объяснение:
Так как 3 раскладывается на целые сомножители как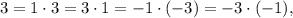
то получаем четыре системы уравнений:
Пошаговое решение:
1. Для начала, перенесем все члены уравнения на одну сторону:
xy + 4x - 2y - 7 - 4 = 0
xy + 4x - 2y - 11 = 0
2. Заметим, что в уравнении есть два переменных: x и y. Нам нужно выразить одну из переменных через другую. Давайте попробуем выразить x через y.
Для этого мы приведем уравнение к виду: x = выражение относительно y.
3. Для начала, выделим общие множители в первых двух членах уравнения:
x(y + 4) - 2y - 11 = 0
4. Теперь, выразим x через y, разделив обе части уравнения на (y + 4):
x = (2y + 11) / (y + 4)
5. Итак, мы нашли выражение для x через y.
Таким образом, решение уравнения xy + 4x - 2y - 7 = 4 в целых числах выглядит следующим образом:
x = (2y + 11) / (y + 4).
Пояснение: Мы использовали метод алгебраических преобразований, чтобы перенести все члены уравнения на одну сторону, чтобы получить выражение для x через y. Это позволяет нам найти значения x и y, удовлетворяющие уравнению.