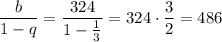486
Объяснение:
Пусть первый член прогрессии равен b, а знаменатель — q. Тогда члены, стоящие на нечётных местах, образуют прогрессию b, bq², bq⁴..., их сумма равна , а члены, стоящие на чётных местах — bq, bq³, bq⁵..., их сумма равна . По условию .
Сумма первых пяти членов прогрессии равна .
Сумма бесконечно убывающей прогрессии равна
486
Объяснение:
Пусть первый член прогрессии равен b, а знаменатель — q. Тогда члены, стоящие на нечётных местах, образуют прогрессию b, bq², bq⁴..., их сумма равна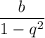 , а члены, стоящие на чётных местах — bq, bq³, bq⁵..., их сумма равна
, а члены, стоящие на чётных местах — bq, bq³, bq⁵..., их сумма равна 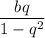 . По условию
. По условию 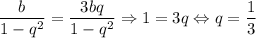 .
.
Сумма первых пяти членов прогрессии равна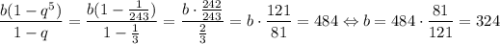 .
.
Сумма бесконечно убывающей прогрессии равна