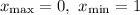Построим высоту СН к стороне АВ. в прямоугольном треугольнике СВН угол В = 45 градусов (по условию), тогда угол ВСН = 90 - 45 = 45 градусов => треугольник равнобедренный, ВН = СН. известно, что ВС = 6, пусть АН = ВН = х, тогда по теореме Пифагора ВС^2 = ВН^2 + СН^2 36 = х^2 + x^2; 36 = 2x^2; x^2 = 18; х = корень из 18;
треугольник АНС - прямоугольный. угол А = 60 градусов (по условию), тогда угол НСА = 90 - 60 = 30 градусов. пусть АС = 2х, тогда АН = х (так как катет, лежащий против угла, равного 30 градусов, равен 1/2 гипотенузы). по теореме Пифагора АС^2 = АН^2 + НС^2 4х^2 = 18 + х^2; 4х^2 - х^2 = 18; 3х^2 = 18; х^2 = 6; х = корень из 6; тогда Ас = 2х = 2 корня из 6 ответ: 2 корня из 6
Достаточные условия экстремума: если при переходе через критическую точку производная непрерывной функции меняет знак на противоположный, то имеем экстремум функции в этой точке.
Если точка с абсциссой меняет знак с "+" на "–" (двигаясь в направлении увеличения ), то — точка максимума, а если с "–" на "+" , то — точка минимума.
в прямоугольном треугольнике СВН угол В = 45 градусов (по условию), тогда угол ВСН = 90 - 45 = 45 градусов => треугольник равнобедренный, ВН = СН.
известно, что ВС = 6, пусть АН = ВН = х,
тогда по теореме Пифагора ВС^2 = ВН^2 + СН^2
36 = х^2 + x^2; 36 = 2x^2; x^2 = 18; х = корень из 18;
треугольник АНС - прямоугольный.
угол А = 60 градусов (по условию), тогда угол НСА = 90 - 60 = 30 градусов.
пусть АС = 2х, тогда АН = х (так как катет, лежащий против угла, равного 30 градусов, равен 1/2 гипотенузы).
по теореме Пифагора АС^2 = АН^2 + НС^2
4х^2 = 18 + х^2; 4х^2 - х^2 = 18; 3х^2 = 18; х^2 = 6; х = корень из 6;
тогда Ас = 2х = 2 корня из 6
ответ: 2 корня из 6
Необходимые условия экстремума:
Имеем две критические (стационарные) точки: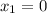
и 
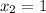
Достаточные условия экстремума: если при переходе через критическую точку производная непрерывной функции меняет знак на противоположный, то имеем экстремум функции в этой точке.
Если точка с абсциссой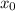
меняет знак с "+" на "–" (двигаясь в направлении увеличения 
), то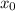 
— точка максимума, а если с "–" на "+" , то 
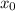— точка минимума.
Из промежутка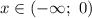
выберем, например, 
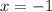и имеем: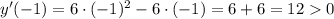 
Из промежутка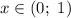
выберем, например, 
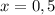и имеем: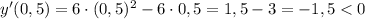 
Имеем максимум в точке с абсциссой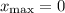
Из промежутка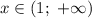
выберем, например, 
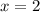и имеем: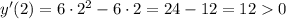 
Имеем минимум в точке с абсциссой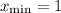
ответ: