Розкладіть на множники квадратний тричлен:
1)bквадратний -15б+14
2) 30у квадратний -10у-100
Розв'яжіть рівняння
1) х у четвертій степені -82х квадрат +81=0
Потрібно розв'язати так щоб не подумали що я списав

Показать ответ

Ответ:

кактыдумаешьотом

25.05.2023 10:35

Само решение написано с красной строки, остальное (кроме ОДЗ) - пояснения.

ОДЗ: т.к. знаменатель не равен 0,

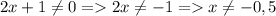
1) $2x+1\neq 0 = 2x\neq -1=x\neq -0,5$

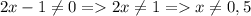
2) $2x-1\neq 0=2x\neq 1=x\neq 0,5$

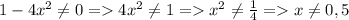
3) $1-4x^2\neq 0 = 4x^2\neq 1= x^2\neq \frac{1}{4}=x\neq 0,5$

Здесь задание на применение формулы разности квадратов, которая выглядит следующим образом: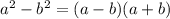 a^2-b^2=(a-b)(a+b) .

$\frac{2x-1}{2x+1}=\frac{2x+1}{2x-1}+\frac{4}{1-4x^2}$

Перенесем все для удобства в левую часть.

$\frac{2x-1}{2x+1}-\frac{2x+1}{2x-1}-\frac{4}{1-4x^2}=0$

Теперь приведем две первые дроби к общему знаменателю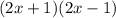 (2x+1)(2x-1) .

$\frac{(2x-1)(2x-1)}{(2x+1)(2x-1)}-\frac{(2x+1)(2x+1)}{(2x-1)(2x+1)}-\frac{4}{1-4x^2}=0$

Запишем их в одну общую дробь.

$\frac{(2x-1)(2x-1)-(2x+1)(2x+1)}{(2x+1)(2x-1)}-\frac{4}{1-4x^2}=0$

Заметим, что в знаменателе вычитаемого тоже есть формула разности квадратов, т.е.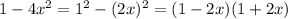 1-4x^2=1^2-(2x)^2=(1-2x)(1+2x)

В уменьшаемом раскроем скобки в числителе с формул квадрата разности и квадрата суммы:

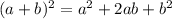
1) $(a+b)^2=a^2+2ab+b^2\\$

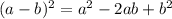
2) (a-b)^2=a^2-2ab+b^2

$\frac{(4x^2-2*2x+1)-(4x^2+2*2x+1)}{(2x+1)(2x-1)}-\frac{4}{(1-2x)(1+2x)}=0$

Раскроем скобки в числителе первой дроби еще раз и упростим получившееся выражение.

$\frac{4x^2-4x+1-4x^2-4x-1}{(2x+1)(2x-1)}-\frac{4}{(1-2x)(1+2x)}=0$ $\frac{0}{(2x+1)(2x-1)}-\frac{4}{(1-2x)(1+2x)}=0$

Теперь перенесем вычитаемое в правую часть и решим уравнение пропорцией.

$\frac{0}{(2x+1)(2x-1)}=\frac{4}{(1-2x)(1+2x)}0(1-2x)(1+2x)=(2x+1)(2x-1)*4\\(2x+1)(2x-1)*4=0\\(2x+1)(2x-1)=0:4\\(2x+1)(2x-1)=0\\\left \{ {{2x+1=0} \atop {2x-1=0}} \right. = \left \{ {{2x=-1} \atop {2x=1}} \right.=\left \{ {{x=-0,5} \atop {x=0,5}} \right.$ (в последней строке скобки должна быть не {, а [, редактор не позволяет их поставить, к сожалению)

Оба корня не подходят по ОДЗ => решений нет, ∈∅

ответ: ∈∅.

0,0(0 оценок)

Ответ:

SuperMan87

10.12.2022 05:36

ответ: -3; -4; х=2

Объяснение:

(х-1)(х²+6х+9)=5(х+3)

(х-1)(х+3)²=5(х+3)

((х-1)*(х+3)-5)(х+3)=0; (х²-х+3х-3-5)(х+3)=0

х+3=0⇒; х=-3; х²-х+3х-3-5=0; х²+2х+1-1-8=0; (х+1)²-9=0; ⇒(х+1)=±3,

х=- 1+3=2; х=-1-3=-4;

ответ -4; -3; 2

проверим, что х=-3- корень уравнения, он правую и левую часть превращает в нуль. сократим на (х+3), получим (х-1)(х+3)=5; раскроем скобки и решим квадратное уравнение. х²+3х-х-3-5=0;

х²+2х-8=0; По Виету х= -4; х=2

ответ -3; -4; х=2

раскроем скобки х³+6х²-9х-х²-6х-9=15х+15

х³+6х²+9х-х²-6х-9-5х-15=0

х³+5х²-2х-24=0

(х³-8)+(5х²-2х-16)=0; 5х²-2х-16=0; х=(1±√(1+80))5=(1±9)/5; х= 2; х=-8/5;

5х²-2х-16=5*(х+8/5)*(х-2)=(5х+8)*(х-2);

(х-2)(х²+2х+4)+(5х+8)*(х-2)=0⇒(х-2)(х²+2х+4+5х+8)=0; х-2=0; х=2

х²+7х+12=0, по Виету х= -4; х=-3

ответ: -3; -4; х=2

0,0(0 оценок)

Популярные вопросы: Алгебра